SSD: Single Shot MultiBox Detector 리뷰
Wei Liu 외 5 명의 저자가 쓴 논문으로, ECCV 2016에 accept된 논문이다.
SSD는 2-stage detector인 Faster R-CNN과 1-stage detector인 YOLOv1의 단점은 보완하고, 장점은 가져와 정확도와 속도에서 큰 성공을 거둔 모델이다.
논문에서는 비교적 rough하게 설명이 되어있어 이해하는데 꽤나 어려움을 겪었는데, 하나하나 디테일하게 뜯어보면서 확실히 이해를 해보자.
Introduction
- Faster R-CNN과 같이 bounding box를 예측한 후에 classify를 적용하는 2-stage detector는 비교적 정확하나(73.2mAP) 느림(7FPS)
- YOLOv1과 같은 1-stage detector는 빠르지만(45FPS) 정확도가 낮음
- 이 논문에서 제안하는 SSD의 경우 정확도와 속도 모두 우월한 성능을 보임(59FPS, 74.3%)
- 속도 향상의 근본적 이유는 region proposal과 pixel/feature resampling과정을 제거했기 때문
- 작은 크기의 convolutional filter를 이용해 정해진 크기와 비율의 다양한 default bounding box의 category score과 box offset을 예측
- 다양한 크기의 feature map으로부터 prediction을 하여 정확도 향상
The Single Shot Detector (SSD)

- SSD는 학습 시 input image와 ground truth box만을 필요로 한다.
- 위 그림처럼 8x8, 4x4와 같이 여러 feature map에서, 그리고 각 location(feature map의 한 cell)마다 정해진 개수(e.g. 4)의 default box를 생성한다.
- 각각의 default box에 대해 offset과 confidence를 예측한다.
- Training 할 때는, 이 default box를 해당하는 ground truth box와 matching해야함. 위의 그림을 예로 들면, 두 개의 파란색 박스(cat), 한 개의 빨간 박스(dog)를 매칭하고 이 박스들은 positive로 두고, 나머지 박스들은 negative로 둔다.
Model
▪ Multi-scale feature maps for detection
기존 backbone network의 뒤쪽을 자르고 convolutional layer를 이어붙여 네트워크를 구성했으며, 네트워크를 따라 feature map의 사이즈가 줄어들게 된다. 따라서 중간중간에 여러 사이즈의 feature map을 detection에 사용할 수가 있다.
▪ Convolutional predictors for detection

위 네트워크 그림의 화살표를 잘 보면, 여러 사이즈의 feature map, 즉 여러 convolutional layer를 이용해서 detection predction을 만들어낼 수 있다. 만약 feature map의 크기가 $m\times{n}\times{p}$ 라고 하면, kernel은 $3\times3\times{p}$ 의 크기를 가지게 되고, 이 kernel은 각 category(class)에 대한 score와, default box의 좌표로부터의 offset을 예측하는데 사용된다. Convolution과정에서 padding 을 1만큼 주게 되므로 가로세로의 크기는 유지하되, 채널만 바뀌게 된다.
그런데 여기서 bounding box의 offset을 예측하는 이유는 다음과 같다.

아까 위에서 본 그림을 가져와서 설명해보면, 우측에 $8\times8$ 크기의 feature map에서 만들어지는 default box가 실제 ground truth box와 크기가 같을 수는 없다. 여기서 default box는 Faster R-CNN의 anchor box를 가져온 것인데, 이 box는 "매개체" 역할을 하는 것이라고 생각하면 된다. 즉 위 한 이미지의 ground truth box 중 하나인 파란색 박스(cat)와 Jaccard overlap(IoU)이 큰 박스들을 선택하고, 이 default box로부터 ground truth box가 얼만큼 떨어져있는지 나타내는 offset을 가지는 지를 모델에 학습시키는 것이다.
▪ Default boxes and aspect ratios
앞서 여러 크기의 feature map(여러 conv layer로부터 나온)을 이용해 detection을 수행한다고 했었다. 이 때, 각 feature map의 cell마다 정해진 개수의 default bounding box를 만들게 되고, $3\times3$ 크기의 kernel을 1의 padding을 가지고 convolution을 수행하게 되므로 모든 cell 마다 정해진 개수의 default box를 가지게 된다. 각 cell 마다 만들어내는 default box와 ground truth box와의 offset을 예측하게 되고, 뿐만 아니라 그 박스에 어떤 class가 존재할 class별 score도 예측한다.
논문에서는 각 location(feature map의 각각 cell)에서 k개의 box가 생성된다고 소개하고 있다. 따라서 해당 default box로부터의 offset을 의미하는 벡터인 $(c_x, c_y, w, h)$ 를 예측하고, 또 총 c 개의 class가 있으므로 $(c+4)k$ 개의 filter가 각 location마다 적용된다. 따라서 Feature map의 가로세로 $m, n$ 까지 $(c+4)kmn$ 개의 output이 나오게 된다. 논문에서는 이러한 default box가 Faster R-CNN에서의 anchor box와 유사하다고 하지만, 여러 resolution에서 적용했기 때문에 차이점이 있다고 소개한다.
Training
▪ Matching strategy
Training 과정에서 네트워크를 잘 학습시키려면, 과연 어떤 default box들이 ground truth box에 상응하는지를 결정해줘야 한다.
먼저, 각각 ground truth box에 대해서 가장 높은 jaccard overlap(IoU)를 가지는 default box는 매칭을 해준다. 다만, Multibox논문에서와는 다르게, jaccard overlap이 threshold(0.5)를 넘는 default box들도 해당 ground truth box와 매칭을 해준다.
이와 같은 matching strategy는 학습의 문제를 좀 더 단순화하고 수월하게 한다고 논문에서 소개하고 있는데 그 이유에 대해서 다음과 같이 주장하고 있다. 각 ground truth box에 대해서 maximum overlap 을 가지는 하나의 default box를 이용하는 것보다, threshold를 넘는 여러 개의 overlapping된 default box들을 이용하면 더욱 정확하게 ground truth box를 예측할 수 있다는 것이다.
▪ Training objective
SSD의 loss function은 MultiBox 논문의 loss function 에서 착안했지만, 더 많은 class의 객체를 위해서 약간 확장된 형태이다.
\[L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+{\alpha}L_{loc}(x,l,g))\]
위 loss function은 localization loss와 confidence loss가 weighted sum된 형태임을 확인할 수 있다(N은 match가 된 default box의 개수, 한 ground truth box의 1개 이상의 default box가 매칭될 수 있기 때문).
$x_{ij}^{p}=\{1, 0\}$ 가 $i$번째 default box가 $p$ class에 해당하는 $j$번째 ground truth box에 매칭되는지를 나타낸다고 해보자. 하나의 ground truth box는 반드시 수 많은 default box 중 하나에는 매칭이 되므로 $\sum_{i}x_{ij}^{p}\geq{1}$ 를 만족한다.
\[L_{loc}(x,l,g)=\sum_{i\in{Pos}}^N\sum_{m\in\{cx,cy,w,h\}}x_{ij}^{k}{smooth_{L1}}(l_i^m-\hat{g}_j^m)\]
\[\hat{g}_j^{cx}=(g_j^{cx}-d_i^{cx})/d_i^{w},\hspace{1cm} \hat{g}_j^{cy}=(g_j^{cy}-d_i^{cy})/d_i^{w}\]
\[\hat{g}_j^{w}=\log{(\frac{g_j^w}{d_i^w})},\hspace{1cm} \hat{g}_j^{h}=\log{(\frac{g_j^h}{d_i^h})}\]
여기서 $L_{loc}$ 은 predicted box ($l$)과 $\hat{g}_j$간의 Smooth L1 loss 이고, Faster R-CNN과 마찬가지로, 모델은 default bounding box ($d$)의 center인 $(cx, cy)$ 와 width $w$와 height $h$ 로부터의 offset을 regress하게 된다. cx, cy, w, h를 위와 같이 두는 것에 대해서는 논문에서도 잘 소개되어있지 않고 empirical하게 얻은 것이라고 생각하면 된다. 그래서 대부분의 detection 학습시에 이와 같은 방법을 관례적으로 따르는 것 같다.
\[L_{conf}(x,c)=-\sum_{i\in{Pos}}^{N}x_{ij}^{p}\log{(\hat{c}_i^p)}-\sum_{i\in{Neq}}\log{(\hat{c}_i^0)}\hspace{0.5cm}\text{where}\hspace{0.5cm}\hat{c}_i^p=\frac{\exp{(c_i^p)}}{\sum_p{\exp{(c_i^p)}}}\]
Confidence loss의 경우에는 여러 class들의 confidence에 대한 softmax를 적용한 것이며, $\alpha$의 경우에는, cross validation을 통해 1로 산출을 했다고 한다.
▪ Choosing scales and aspect ratios for default boxes
Semantic segmentation의 여러 논문들이 lower layer에서 입력 object의 fine한 특징을 잡아내는 것과, feature map의 pooling으로부터 global context를 잡아내는 등의 성과를 내자 여기에 착안해 이 논문에서도 lower, upper한 feature map을 모두 사용한다. SSD의 경우, 각 feature map 사이즈에서 특정 scale의 object에 responsive할 수 있도록 해준다. 즉, m개의 feature map이 있다고 했을 때, 각각의 default box의 scale은 아래와 같이 계산된다.
\[s_k=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1),\hspace{0.5cm}k\in[1,m]\]
$s_{min}$은 0.2, $s_{max}$는 0.9이고, 각각 가장 low한 layer와 high한 layer에서 0.2, 0.9의 scale을 가짐을 의미한다. 중간의 layer들은 같은 간격으로 크기를 가지는 것도 수식을 통해 알 수 있다.
실제 구현을 하려면, 이 scale과 ratio 부분이 중요하다.
각 default box들에게 다른 aspect ratio를 부여하는데($a_r\in\{1,2,3,\frac{1}{2},\frac{1}{3}\}$),
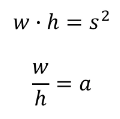
이를 통해 각 default box의 width($w_k^a=s_k{\sqrt{a_r}}$) 와 height($h_k^a=s_k/{\sqrt{a_r}}$) 를 계산할 수 있다. 특별히 aspect ratio가 1인 경우, scale이 $s_k^\prime=\sqrt{s_{k}s_{k+1}}$인 default box를 추가해줘서 총 6개의 default box를 location마다 가지게 된다. 여기서 default box의 센터 좌표를 $(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|})$ 로 설정했는데($|f_k|$는 k번째 feature map의 한 변의 크기), 이 또한 empirical 한 것이라고 논문에서 소개하고 있다.
▪ Hard negative mining
매칭 과정이 끝나고 나면, 대부분의 default box들은 negative로 분류가 된다. 특히나 default box의 개수가 많을수록 negative의 수가 훨씬 많기 때문에 positive, negative training examples 간의 imbalance가 생기게 된다. 따라서 모든 negative examples를 쓰는 게 아니라, confidence loss가 높은 순으로 정렬을 해서 가장 hard한 negative example들을 뽑아내고 최대 neg:pos=3:1의 비율로 뽑아낸다. 논문에서는 이러한 hard negative mining 기법이 더 빠른 최적화와 더 안정적인 학습을 하는 데 도움을 준다고 소개하고 있다.
▪ Data augmentation
다양한 input object의 size와 shape에 모델이 더 robust하게 detect할 수 있도록 각 training image는 아래의 option중 하나를 따르게 된다.
- original input image 를 그냥 그대로 쓰는 것
- 객체와의 minimum jaccard overlap이 0.1, 0.3, 0.5, 0.7, 0.9 가 되도록 image안의 patch를 샘플링
- 랜덤하게 patch를 샘플링
샘플링된 patch의 사이즈는 원본 이미지의 [0.1, 1] 배가 되고, aspect ratio는 $\frac{1}{2}$, 2 이다.
더 나아가 resizing, horizontally filp($p$=0.5), photo-metric distortion 등의 augmentation도 적용된다.
Experimental Results
PASCAL VOC2007
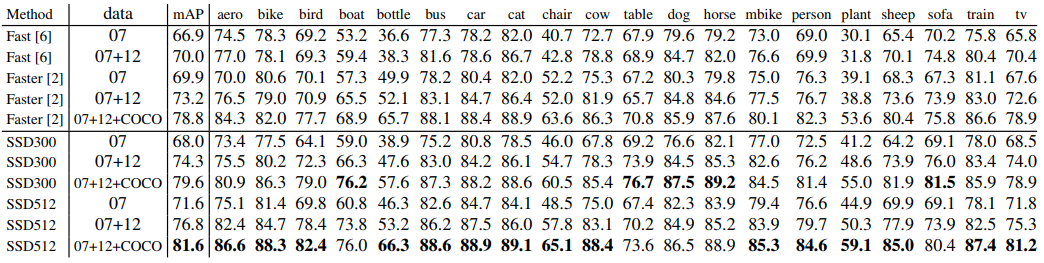
- SSD300 이 Fast R-CNN 보다 높은 성능을 보인다.
- $512\times512$ input image로 학습시킨 SSD512는 Faster R-CNN 보다 높은 성능을 보인다.
- 더 많은 data (07+12)로 학습시켰을 때는 SSD300이 Faster R-CNN보다 1.1%, SSD512는 3.6%나 높은 성능을 보인다.
- COCO trainval 데이터셋으로 SSD512를 학습시킨 뒤 PASCAL 07+12로 fine-tuning했을 때, SOTA를 달성했다.(81.6% mAP)
Model analysis
아래는 $300\times300$ input size로, ablation study를 진행한 결과 테이블이다.

▪️ 데이터 증강은 필수적이다
Data augmentation을 했냐 안했느냐에 따라 8.8%의 차이가 난다.
▪️ Default box shape이 많을 수록 더 좋다
Default box는 원래 6개인데, $\{\frac{1}{3}, 3\}$과 $\{\frac{1}{2},2\}$를 연달아 없애서 실험해본 결과 0.6%, 거기에 더해 2.1% 까지 더 mAP가 떨어지는 것을 확인할 수 있다.
▪️ Atrous 기법이 더 빠르다
일반적인 conv layer를 쓸 때보다 a trous algorithm을 쓴 경우 mAP는 비슷하나 속도 측면에서 20% 더 빠르다.

▪️ 다양한 resolution으로부터 multiple output layer가 나오는 게 더 좋다
SSD의 주 contribution 또한 다른 output layer로부터 나오는 다른 크기의 default box 사용이다.
“Use boundary boxes?” 는 Faster R-CNN에서 쓰인 기법처럼 경계선에 걸친 box를 쓸 거냐는 것인데,
coarse feature map(conv11_2) 이 큰 차이로 정확도가 떨어지는 이유는, 큰 object를 커버할 수 있는 box들이 pruning에 의해 날라가기 때문이라고 이해하면 된다.
PASCAL VOC2012
2007 의 경우와 같이 setting하나, 여기서는 VOC2012 trainval, VOC2007의 trainval과 test 모두를 trian에 사용했고,
VOC2012의 test 데이터셋을 test에 사용했다.

성능 경향은 VOC2007 데이터셋을 사용했을 때와 크게 다르지 않다.
COCO
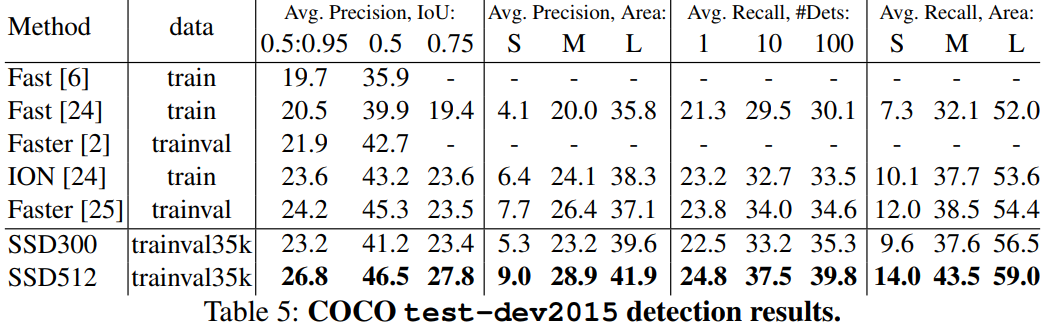
COCO의 object가 더 작은 경향이 있으므로 default box의 scale을 좀 더 낮춰서 실험을 진행하였다.
COCO dataset에 대해서도 sota 달성하는 것을 확인할 수 있다
