CH01. Camera Models (1)
Pinhole cameras

그림에서처럼, 3D 물체의 각각의 point는 여러 광선을 배출한다.
장벽이 없으면, film의 모든 점이 3D object의 모든 점으로부터 영향을 받겠지만, 장벽과 작은 틈으로 인해 하나 또는 몇 개의 ray만 통과할 수 있다.
따라서 3D object와 film 의 각 point 사이의 one-to-one mapping이 가능하다.
결과적으로 film은 이 mapping덕에 “image”를 얻게 되고, 이러한 simple한 모델을 pinhole camera model이라고 부른다.

Pinhole camera를 좀 더 formal하게 나타내면 위의 그림과 같이 나타낼 수 있다.
먼저 용어 정리를 할 필요가 있다.
위 구조에서 film은 image 또는 retinal plane 이라고 불린다.
틈(aperture)은 여기선 pinhole 로써 $O$라고 부르거나, center of the camera라고 부르며,
Image plane과 pinhole $O$ 사이의 거리를 focal length $f$ 라고 부른다.
Retinal plane이 $O$와 3D object 사이에 존재할 수도 있는데 (실제로 그런 건 아님 가상으로) 이걸 virtual image 또는 virtual retinal plane이라고 한다.

그렇다면 어떻게 pinhole camera를 이용할까.
위의 점 $P$를 $P=[x \,\,\, y\,\,\,z]^T$ 를 pinhole camera에서 보이는 3D object의 한 점이라고 하자.
$P$는 image plane $\Pi^\prime$에 $P^\prime=[x^\prime\,\,\,y^\prime]^T$으로 project된다.
비슷하게, pinhole 또한 image plane에 $C^\prime$으로 project된다.
Image plane과 perpendicular한(수직한) 축 k를 포함해 pinhole $O$로부터 coordinate system $[i\,\,\,j\,\,\,k]$를 정의하고, 이 coordinate system을 camera reference system 또는 camera coordinate system이라고 부른다.
또한 $C^\prime$과 $O$를 잇는 선을 camera system의 optical axis 라고 부른다.
$P^\prime$은 3D 점인 $P$가 image plane $\Pi^\prime$ 으로 project된 것이므로, $P$와 $P^\prime$의 관계를 잘 정리하면, 어떻게 3D world가 pinhole camera를 통해 image에 찍히는 지 이해할 수 있다.
삼각형 $P^\prime C^\prime O$는 점 $P, O$ 그리고 $(0,0,z)$로 형성된 삼각형과 닮음이므로 닮음비를 이용하면
$$ \begin{align}P^\prime=[x^\prime\,\,\,y^\prime]^T=[f\frac{x}{z}\,\,\,f\frac{y}{z}]^T\end{align} $$
이 성립한다.
주의해야 할 점은, 우리는 pinhole model에서 이 aperture(틈)을 single point로 가정한다는 것인데, 실제로 real world에서는 이 aperture가 무한히 작다고 가정을 할 수가 없다.
그렇다면 먼저 다양한 aperture size에 따른 차이를 살펴보자.

먼저, Aperture의 크기가 증가할수록 통과하는 ray의 수가 많아지게 되고, film위의 각각의 point들은 3D space로부터의 여러 light ray에 영향을 받게 돼 image가 blur된다.(흐려짐)
반대로 aperture의 크기를 가능한 최대로 줄이고 싶을 수도 있는데, 그렇게 되면 barrier을 통과하는 light ray의 수가 줄어들게 되고 좀 더 깨끗하지만 어두운 image를 얻게 된다.
따라서 가장 근본적인 문제에 맞닥뜨리게 되는데, 과연 crisp(맑은) 하면서도 bright 한 image를 얻을 수 있는 camera를 어떻게 만드냐는 것이다.
Cameras and lenses
Modern한 camera에서는, 위에서의 crispness와 brightness 사이의 trade off를 lens(빛을 focus하거나 disperse할 수 있는 device)를 이용해서 완화한다.
즉 pinhole을 대신해 lens를 적절한 사이즈로 적절히 배치하기만 하면 다음과 같은 property를 만족하게 된다.
어떤 점 $P$로부터 나오는 모든 light ray가 lens에 의해 굴절돼 결국 image plane위의 한 점인 $P^\prime$ 으로 수렴하게 된다는 것이다.

따라서 small aperture로 인해 대부분의 light ray가 막혔던 문제가 해결된다.
하지만 주의할 점은, 이 property가 모든 3D point에 만족하는 것은 아니다.
예를 들어 $P$보다 image plane으로부터 더 가깝거나 더 먼 다른 한 점 $Q$를 생각해보면, 그 점의 image로의 projection은 흐리거나 초점이 나갈 것이다.(파란 점과 같이)
따라서 lens는 어떠한 object가 초점이 맞춰질 수 있도록 하는 특정한 distance가 있다는 뜻이다.

이러한 property는 photography와 computer graphics에서의 depth of field라는 개념과도 관련이 있다.
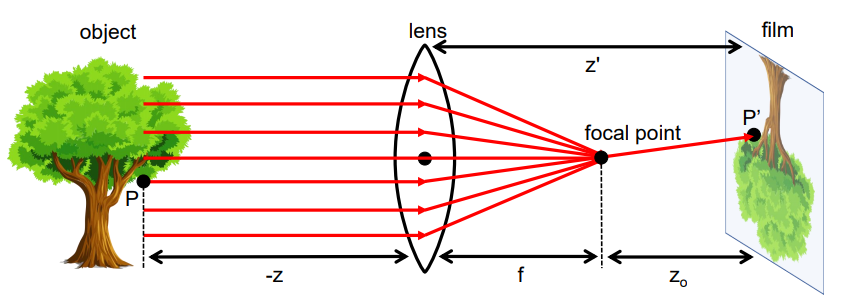
Camera lens는 또 다른 흥미로운 property를 갖고 있다.
위의 그림처럼 camera lens는 optical axis와 평행한 모든 light ray를 focal point라고 하는 한 점으로 focus 시킨다는 것이다.
Focal point와 lens의 중심과의 거리는 보통 focal length $f$라고 부른다(앞에서의 focal length는 pinhole camera model에서고, 이건 lens model임).
더 나아가 렌즈의 중심을 지나는 light ray들은 deviate되지 않고 그대로 나아간다(굴절 없음).
따라서 pinhole model과 비슷하게, 3D space의 점 $P$와 상응하는 image plane의 점 $P^\prime$ 의 관계를 정립해볼 수 있다.
$$ \begin{align}P^\prime=\begin{bmatrix}x^\prime \\ y^\prime\end{bmatrix}=\begin{bmatrix}z^\prime\frac{x}{z} \\ z^\prime\frac{y}{z}\end{bmatrix}\end{align} $$
강의자료에는 아래와 같은 그림이 설명으로 주어지는데,
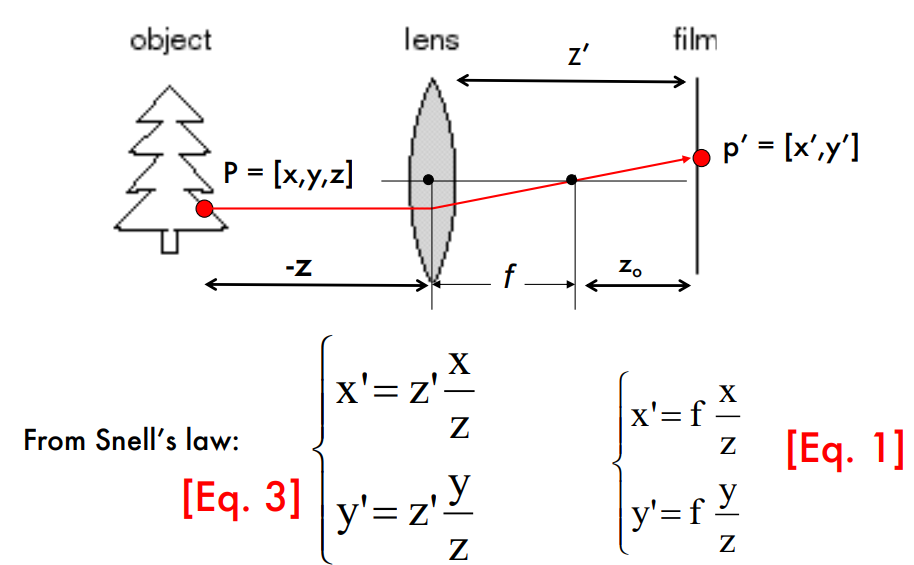
이해가 안돼서 좀 찾아봤는데, 그림을 다음과 같이 고치는 게 맞는 것 같다.
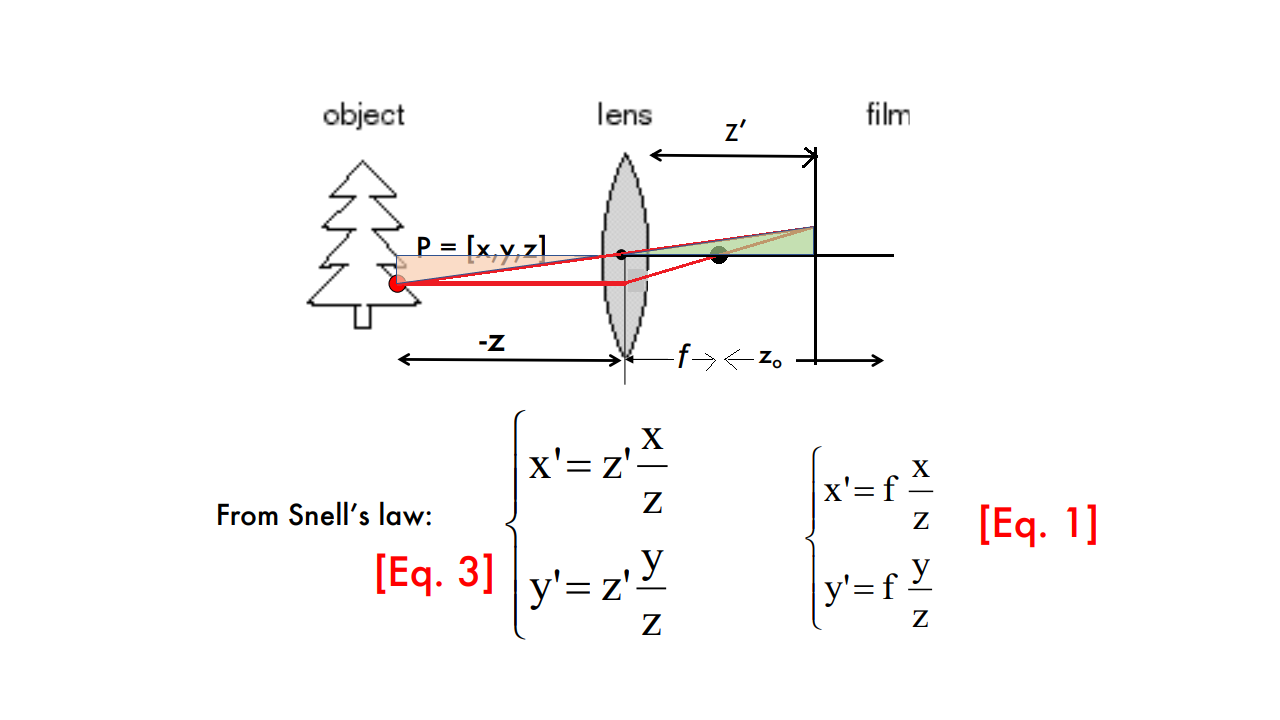
위 그림과 같이 그려야 닮음이 성립한다.
처음에 그림을 보고 이해가 안됐는데, 위 그림처럼 그리니 이해가 됐다.
유의할 점은, pinhole model에서는 $z^\prime=f$ 이지만, 지금처럼 lens-based model에서는 $z^\prime=f+z_0$ 이다.
또, 위의 유도가 paraxial 또는 “thin lens” 를 가정하므로, 이를 paraxial refraction model 이라고 부른다.
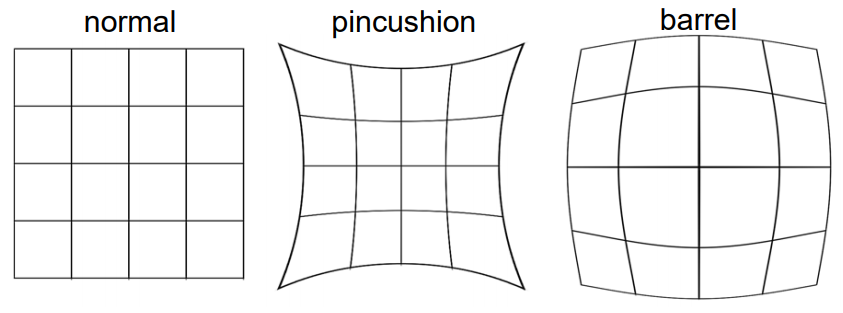
이와 같이 thin lens model을 이용해서 paraxial refraction model에 근사하는 것이기 때문에, normal하지 못한 경우가 생길수도 있다.
가장 일반적인 경우가 radial distortion(방사왜곡)이다.
Radial distortion은 optical axis까지의 거리에 따라 image의 magnification을 유발하는 왜곡으로, pincushion distortion과 barrel distortion으로 나뉜다.
이러한 Radial distortion은 lens의 다른 부분들이 서로 다른 focal length를 가지고 있을 때 나타나는 현상으로, pincushion의 경우에는 magnification이 increase하고, barrel의 경우에는 magnification이 decrease한다.