CH01. Camera Models (3)
Camera Calibration
앞에서 intrinsic, extrinsic parameter 를 알아야 정확한 transformation이 가능하다고 했다.
하지만 임의의 카메라를 처음 쓰게 되면, parameter들에 대한 정보가 없다.
하지만 그 카메라로 image를 촬영할 수는 있다.
따라서 해당 image를 이용해 extrinsic, intrinsic camera parameter들을 추정하는 것이 바로 camera calibration이다.

위의 사진은 calibration rig 를 보여준다.
이 rig는 보통 그림처럼 차원을 가진 simple한 패턴으로 구성되고,
더 나아가 rig는 world reference를 원점 $O_w$ 와 $i_w,j_w,k_w$ 로 정의한다.
이 때, world reference frame에서 우리가 알고있는 점들 $P_1, ...,P_n$ 이 주어지고,
해당 점들에 상응하는 image의 점들 $p_1,...,p_n$을 직접 찾아준다.
그 후, n개의 3D, 2D 포인트 쌍으로부터 아래와 같이 linear system of equations을 유도해낸다.
$$ p_i=\begin{bmatrix}u_i \\ v_i\end{bmatrix}=MP_i=\begin{bmatrix}\frac{m_1P_i}{m_3P_i} \\ \frac{m_2P_i}{m_3P_i}\end{bmatrix} $$
($m_1,m_2,m_3$ 는 matrix $M$의 각 행을 의미)
위의 식에서 각 $P_i, p_i$ 쌍으로부터 2개의 equations를 얻을 수 있다.
따라서 $m$의 parameter를 풀기위한 2개의 constraint도 얻을 수 있다.
$$ u_i(m_3P_i)-m_1P_i=0 \\ v_i(m_3P_i)-m_2P_i=0 $$
앞에서 camera matrix 는 11개의 unknown parameter가 있다고 했었다.
따라서 6개의 correspondence만 있으면 이 matrix를 찾을 수 있다.
하지만 실제 세상에서는, 정확하게 측정되기 어렵기 때문에 noise가 있을 수 밖에 없다.
$n$개의 correspondence가 주어졌을 때, 전체 linear system of equation은 다음과 같다.
$$ u_1(m_3P_1)-m_1P_1=0 \\ v_1(m_3P_1)-m_2P_1=0 \\ \vdots \\ u_n(m_3P_n)-m_1P_n=0 \\ v_n(m_3P_n)-m_2P_n=0 $$
이걸 matrix-vector product 형태로 바꾸면,
$$ \begin{bmatrix}P_1^T & 0^T & -u_1P_1^T \\ 0^T & P_1^T & -v_1P_1^T \\ &\vdots& \\ P_n^T & 0^T & -u_nP_n^T \\ 0^T & P_n^T & -v_nP_n^T\end{bmatrix}\begin{bmatrix}m_1^T \\ m_2^T \\ m_3^T\end{bmatrix}=\mathbf{P}m=0 $$
(위의 $m$ 벡터는 $M$ 행렬의 모든 행을 열로 펴서 한 열로 만들어 놓은 열벡터이다.)

그런데 $2n>11$ 일 때, 위에서 세운 homongeneous linear system은 overdetermined(미지수보다 방정식이 더 많음)하고,
$m=0$ 은 항상 trivial solution이 된다.
뿐만 아니라 nonzero solution이 아닌 $m$ 에 대해서, $\forall k\in\mathbb{R}$인 $km$이 solution 으로 가능하다.
따라서 solution에 constraint을 줘야한다.
따라서 minimization을 완성시켜보면 다음과 같다.
$$ \underset{m}{\text{minimize}}\,\,\,\,\|\mathbf{P}m\|^2 \\\text{subject to}\,\,\,\,\,\|m\|^2=1 $$
위의 minimization problem을 풀려면, 그냥 singular value decomposition(SVD)를 이용하면 된다.
$P=UDV^T$ 라 했을 때, solution은 $V$의 마지막 column이다. ($m$이 $V$의 마지막 column과 같음)
이렇게 얻은 $m$은 벡터이므로 다시 matrix $M$으로 바꿔야한다.
이 $M$은 true matrix가 아니라 $M$의 scalar multiple이다.
즉 실제 camera matrix는 $K\begin{bmatrix}R&T\end{bmatrix}$ 였으므로
$$ \rho M=\begin{bmatrix} \alpha r_1^T-\alpha\cot\theta r_2^T+c_xr_3^T & \alpha t_x-\alpha\cot\theta t_y+c_xt_z \\ \frac{\beta}{\sin\theta}r_2^T+c_yr_3^T & \frac{\beta}{\sin\theta}t_y+c_yt_z \\ r_3^T & t_z \end{bmatrix} $$
가 된다. ($r_1^T,r_2^T,r_3^T$는 $R$의 행들임)
이를 scaling parameter $\rho$로 나눠주면
$$ M=\frac{1}{\rho}\begin{bmatrix} \alpha r_1^T-\alpha\cot\theta r_2^T+c_xr_3^T & \alpha t_x-\alpha\cot\theta t_y+c_xt_z \\ \frac{\beta}{\sin\theta}r_2^T+c_yr_3^T & \frac{\beta}{\sin\theta}t_y+c_yt_z \\ r_3^T & t_z \end{bmatrix}=\begin{bmatrix}A & b\end{bmatrix}=\begin{bmatrix}a_1^T \\ a_2^T \\ a_3^T\end{bmatrix}\begin{bmatrix}b_1 \\ b_2 \\ b_3\end{bmatrix} $$
이고, $A,b$ 는 다음과 같다.
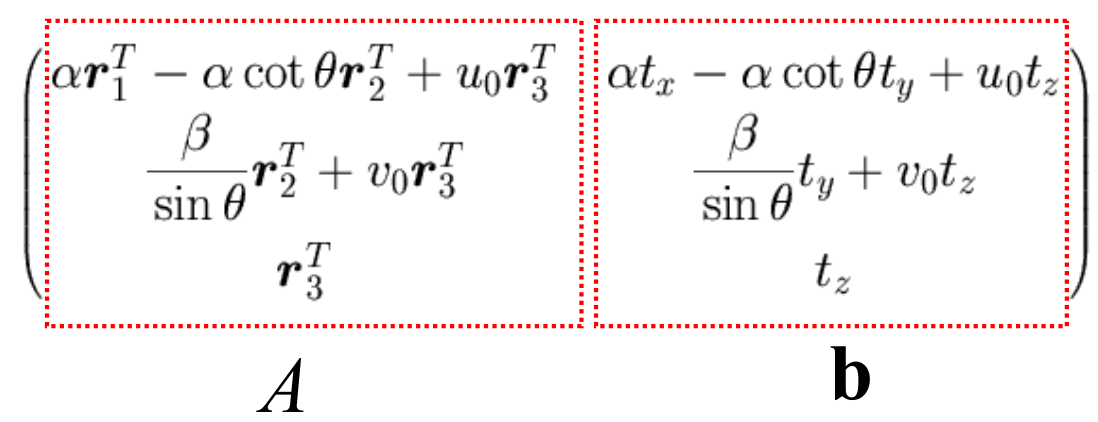
전개해서 풀면 intrinsic parameter는
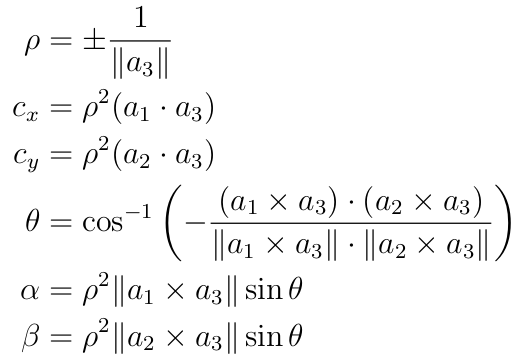
이고, extrinsic parameter는
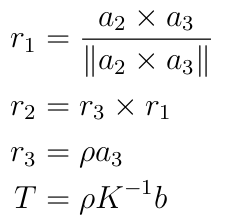
과 같다. (유도 과정은 강의 범위를 벗어나므로 생략)
유의할 점으로는, 위의 과정에서 degenerate case가 발생할 수도 있는데,
예를 들어, 모든 $P_i$ 들이 같은 평면 위에 있으면 안 된다.
이와 같은 점들을 degenerate configurations라고 부른다.