최적화 문제
곡선 적합
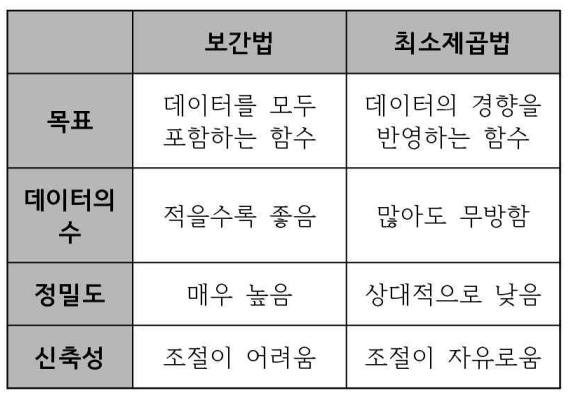
보간법(Interpolation)
개념
주어진 특정 점들을 포함하는 함수를 구하는 방법.
💡 좌표평면에 있는 임의의 서로 다른 $n$개의 점을 지나는 $k$차 다항함수는 유일하게 존재한다. (단, $k$는 $k<n$ 인 자연수)
보간법은 좀 제한적인 개념이다.
즉, 해당 $n$개의 점들을 만족하는 다항함수가 없을 수도 있다.
만약 있다면, 이는 유일하다는 의미이다.
사례
네 점 $(1,3), (2,-2), (3,-5), (4,0)$ 을 모두 지나는 3차 함수
$$ f(x)=a_0+a_1x+a_2x^2+a_3x^3 $$
을 구하자. 우선 다음의 방정식을 세운다.
① $\begin{pmatrix}1&x_1&x_1^2&x_1^3\\1&x_2&x_2^2&x_2^3\\1&x_3&x_3^2&x_3^3\\1&x_4&x_4^2&x_4^3\end{pmatrix}\begin{pmatrix}a_0\\a_1\\a_2\\a_3\end{pmatrix}=\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}$
② 네 점을 대입하고 augmented matrix(첨가행렬)을 만든다.
$\begin{pmatrix}1&1&1&1&3\\1&2&4&8&-2\\1&3&9&27&-5\\1&4&16&64&0\end{pmatrix}$
③ 첨가행렬을 가우스-조던 소거법을 이용해 푼다.
$\begin{pmatrix}1&1&1&1&3\\1&2&4&8&-2\\1&3&9&27&-5\\1&4&16&64&0\end{pmatrix}\Rightarrow\begin{pmatrix}1&0&0&0&4\\0&1&0&0&3\\0&0&1&0&-5\\0&0&0&1&1\end{pmatrix}$
④ $a_0=4,\,\,a_1=3,\,\,a_2=-5,\,\,a_3=1$ 이므로 $f(x)=4+3-5x^2+x^3$ 이다.

앞에서도 설명했지만 보간법의 치명적인 단점은, 유연성이 부족하다.
즉, 머신러닝 용어로 overfitting의 위험이 높다.
최소제곱법(Least squares)
개념
특정 점들을 포함하는 함수를 특정 지을 수 없을 때,
실제 해와의 오차 제곱 합이 최소가 되는 근사적인 해를 구하는 방법.
(보간법처럼 딱 맞을 필요가 없으니 유연성이 좋다)
💡 방정식 $A\text{x}=B$ 을 변형한 방정식 $A^TA\text{x}=A^TB$ (정규방정식)의 모든 해는 $A\text{x}=B$의 최소제곱해이다.
사례
네 점 $(0,1),(1,3), (2,4), (3,4)$ 에 근사하는 일차함수
$$ f(x)=a_0+a_1x $$
을 구하자. 우선 다음의 방정식을 세운다.
① $A\text{x}=B$
$\begin{pmatrix}1&x_1\\1&x_2\\1&x_3\\1&x_4\end{pmatrix}\begin{pmatrix}a_0\\a_1\end{pmatrix}=\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}$
② 네 점을 대입하고 정규방정식 $A^TA\text{x}=A^TB$로부터 방정식 $\text{x}=(A^TA)^{-1}A^TB$을 구성한다.
$A^TA=\begin{pmatrix}4&6\\6&14\end{pmatrix}$ 이므로
$(A^TA)^{-1}=\begin{pmatrix}4&6\\6&14\end{pmatrix}^{-1}=\dfrac{1}{10}\begin{pmatrix}7&-3\\-3&2\end{pmatrix}$
$\therefore\quad\text{x}=\dfrac{1}{10}\begin{pmatrix}7&-3\\-3&2\end{pmatrix}\begin{pmatrix}1&1&1&1\\0&1&2&3\end{pmatrix}\begin{pmatrix}1\\3\\4\\4\end{pmatrix}$
③ $\text{x}=\begin{pmatrix}a_0\\a_1\end{pmatrix}=\begin{pmatrix}\frac{3}{2}\\1\end{pmatrix}$ 이므로 구하고자 하는 함수는 $f(x)=\dfrac{3}{2}+x$ 이다.

$n$차 일반화
$m$개의 자료점 $(x_1,y_1),\cdots,(x_m,y_m)$에 대해 $n$차 다항식 $y=a_0+a_1x+\cdots+a_nx^n$을 최소제곱법으로 이용하여 근사하기 위해서는 $A\text{x}=B$를
$$ A=\begin{pmatrix}1&x_1&\cdots&x_1^n\\1&x_2&\cdots&x_2^n\\\vdots&\vdots&\ddots&\vdots\\1&x_m&\cdots&x_m^n\end{pmatrix},\,\,\text{x}=\begin{pmatrix}a_0\\a_1\\\vdots\\a_n\end{pmatrix},\,\,B=\begin{pmatrix}y_1\\y_2\\\vdots\\y_m\end{pmatrix} $$
로 설정하면 된다.
사실, 위와 같은 꼴의 다항식이 아니라 만약 식이 $xy, \log x, \sin x$ 등의 항이 있다 하더라도 똑같이 적용가능하므로 굉장히 유용하다.
두 방법의 비교
이차형식의 최적화
이차형식(Quadratic form)
가환환 $K$ 위의 가군 $V$에 대해 다음 세 조건을 만족시키는 함수 $Q:V\rightarrow K$
$\forall k,l\in K,\,\,\forall u,v,w\in V,$
- $Q(kv)=k^2Q(v)$
- $Q(u+v+w)=Q(u+v)+Q(v+w)+Q(u+w)-Q(u)-Q(v)-Q(w)$
- $Q(ku+lv)=k^2Q(u)+l^2Q(v)+klQ(u+v)-klQ(u)-klQ(v)$
예1) $R^2$ 상의 일반적인 이차형식은 다음과 같다.
$$ a_1x_1^2+a_2x_2^2+2a_3x_1x_2\Leftrightarrow\begin{pmatrix}x_1&x_2\end{pmatrix}\begin{pmatrix}a_1&a_2\\a_3&a_2\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix} $$
예2) $R^3$ 상의 일반적인 이차형식은 다음과 같다.
$$ a_1x_1^2+a_2x_2^2+a_3x_3^2+2a_4x_1x_2+2a_5x_1x_3+2a_6x_2x_3\\\Leftrightarrow\begin{pmatrix}x_1&x_2&x_3\end{pmatrix}\begin{pmatrix}a_1&a_4&a_5\\a_4&a_2&a_6\\a_5&a_6&a_3\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix} $$
제약된 극값
개념
특정 제약(constraint) 하에 결정되는 원하는 식의 최댓값 또는 최솟값.
💡 $n\times n$ 행렬 $A$의 eigenvalue를 큰 순서대로 $\lambda_1,\cdots,\lambda_n$ 이라 하자. 이 때 $\|\text{v}\|=1$ 제약 하에 $\text{v}^TA\text{v}$ 의 최댓(솟)값은 $\lambda_1(\lambda_n)$에 대응하는 단위고유벡터에서 존재한다.
사례
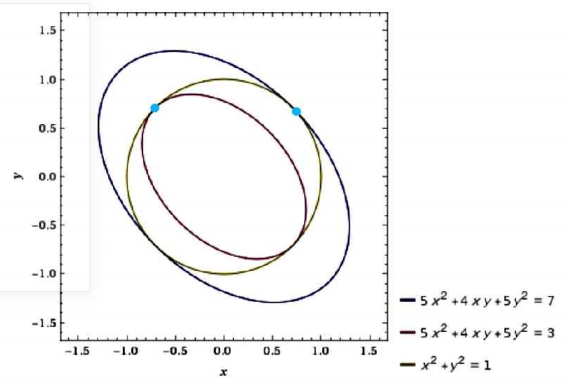
제약 $x^2+y^2=1$ 하에서 $z=5x^2+5y^2+4xy$ 의 최댓값과 최솟값을 구하자.
우선 $z$를 이차형식 $\text{v}^TA\text{v}$ 형태로 변환한다.
① $a_1x^2+a_2y^2+2a_3xy\\\Leftrightarrow\begin{pmatrix}x_1&x_2\end{pmatrix}\begin{pmatrix}a_1&a_2\\a_3&a_2\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=\text{v}^TA\text{v}$
즉, $z=\begin{pmatrix}x&y\end{pmatrix}\begin{pmatrix}5&2\\2&5\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$
② 행렬 $A=\begin{pmatrix}5&2\\2&5\end{pmatrix}$ 의 eigenvalue와 eigenvector를 구한다.
$\lambda_1=7,\quad\text{v}_1=(1,1)\\\lambda_2=3,\quad\text{v}_2=(-1,1)$
③ Eigenvector를 정규화한다.
$\lambda_1=7,\quad\text{v}_1=(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}})\\\lambda_2=3,\quad\text{v}_2=(-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}})$
④ 따라서 $(x,y)=(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}})$ 일 때 $z$는 최댓값 $7$을 갖고,
$(x,y)=(-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}})$ 일 때 $z$는 최솟값 $3$을 갖는다.
※ 물론 nomalize안해도 최대 최소값은 변함없다.