CH03. Epipolar Geometry (2)
The Fundamental Matrix
앞선 강의에서 봤던 Essential matrix 같은 경우는 카메라가 canonical 한 경우($K=I)$에만 해당되므로 canonical한 카메라가 아닌 general한 경우에 대해서도 생각해볼 필요가 있다.
먼저 projection matrix는 다음과 같았다.
$$ M=K\begin{bmatrix}I&0\end{bmatrix}\quad\quad M^\prime=K^\prime\begin{bmatrix}R_{wc^\prime}^{T}&-R_{wc^\prime}^{T}T_{wc^\prime}\end{bmatrix} $$
만약 카메라가 canonical하다면, 각각의 image plane으로의 $P$의 projection은 $p_c=K^{-1}p$ 와 $p_c^\prime=K^{\prime-1}p^\prime$ 이 될 것이다.(여기서 $c$첨자는 camera가 아니라 canonical을 의미함에 주의)
앞서서 canonical한 경우 아래의 식이 성립함을 확인했었다.
$$ p_c^T[T_{\times}]Rp_c^\prime=0 $$
따라서 아래의 식이 유도된다.
$$ p^TK^{-T}[T_{\times}]RK^{\prime-1}p^\prime=0 $$
이 때, $F=K^{-T}[T_{\times}]RK^{\prime-1}$ 를 Fundamental Matrix라고 한다.
Fundamental matrix는 essential matrix와 비슷하지만, 추가적으로 camera matrix $K,K^\prime$의 정보 또한 포함하고 있다는 것이 특징이다.
따라서, transformation 행렬인 $R,T$ 뿐만 아니라 camera matrix $K,K^\prime$를 몰라도 $p,p^\prime$에 대응하는 epipolar line을 계산해낼 수 있다.
Essential matrix와 비슷하게 다음과 같이 $\ell^\prime=F^Tp$ 그리고 $\ell=Fp^\prime$ 와 같이 epipolar line을 구한다.
(Essential matrix의 자유도는 5, Fundamental matrix의 자유도는 7)
Essential matrix와 마찬가지로 fundamental matrix도 이미지 상의 한 점을 아는 것만으로 해당 점에 대응하는 epipolar line이라는 constraint을 준다.
따라서 3D 상의 $P$와 카메라의 extrinsic, intrinsic matrix를 알지 못해도 $p,p^\prime$ 사이의 관계를 세울 수 있다.
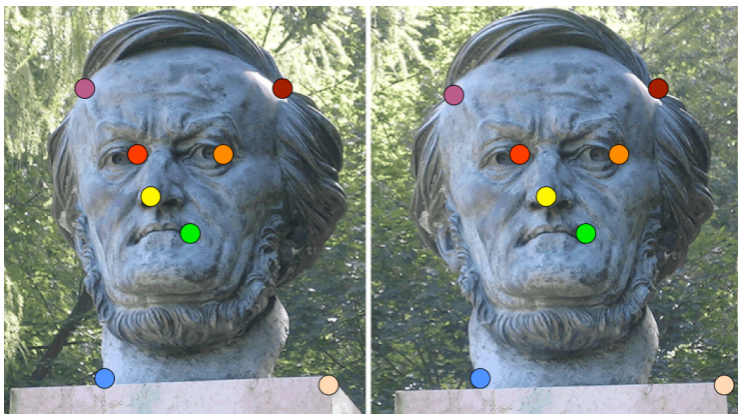
The Eight-Point Algorithm
여태껏 우리가 fundamental matrix를 알고 있다고 가정했는데, 사실 $F$를 몰라도 추정해낼 수 있다.
같은 scene에 대한 두 이미지에서 상응하는 8개의 점만 있다면 $F$를 찾을 수 있는데, 이 방법을 Eight-Point Algorithm이라고 한다.
각 상응하는 점 $p_i=(u_i,v_i,1)$과 $p_i^\prime=(u_i^\prime,v_i^\prime,1)$ 으로 $p_i^TFp_i^\prime=0$ 의 관계가 성립한다.
이를 다음과 같이 쓸 수 있다.
$$ \begin{bmatrix}u_iu_i^\prime&u_iv_i^\prime&u_i&u_i^\prime v_i&v_iv_i^\prime&v_i&u_i^\prime&v_i^\prime&1\end{bmatrix}\begin{bmatrix}F_{11}\\F_{12}\\F_{13}\\F_{21}\\F_{22}\\F_{23}\\F_{31}\\F_{32}\\F_{33}\end{bmatrix}=0 $$
Fundamental matrix의 up to scale 이 아니라 하나로 결정하기 위해서는 8개의 constraint이 필요하다.
($F$의 자유도가 7이라는 게 모르는 값이 7개라는 것은 아님. $F_{11}$부터 $F_{33}$까지 다 모르는데, 이게 homogeneous coordinate이므로 $F_{33}=1$로 고정해줄 수 있음. 따라서 우리가 실제로 모르는 값은 8개임)
$$ \begin{bmatrix}u_1u_1^\prime&u_1v_1^\prime&u_1&u_1^\prime v_1&v_1v_1^\prime&v_1&u_1^\prime&v_1^\prime&1\\u_2u_2^\prime&u_2v_2^\prime&u_2&u_2^\prime v_2&v_2v_2^\prime&v_2&u_2^\prime&v_2^\prime&1\\u_3u_3^\prime&u_3v_3^\prime&u_3&u_3^\prime v_3&v_3v_3^\prime&v_3&u_3^\prime&v_3^\prime&1\\u_4u_4^\prime&u_4v_4^\prime&u_4&u_4^\prime v_4&v_4v_4^\prime&v_4&u_4^\prime&v_4^\prime&1\\u_5u_5^\prime&u_5v_5^\prime&u_5&u_5^\prime v_5&v_5v_5^\prime&v_5&u_5^\prime&v_5^\prime&1\\u_6u_6^\prime&u_6v_6^\prime&u_6&u_6^\prime v_6&v_6v_6^\prime&v_6&u_6^\prime&v_6^\prime&1\\u_7u_7^\prime&u_7v_7^\prime&u_7&u_7^\prime v_7&v_7v_7^\prime&v_7&u_7^\prime&v_7^\prime&1\\u_8u_8^\prime&u_8v_8^\prime&u_8&u_8^\prime v_8&v_8v_8^\prime&v_8&u_8^\prime&v_8^\prime&1 \end{bmatrix}\begin{bmatrix}F_{11}\\F_{12}\\F_{13}\\F_{21}\\F_{22}\\F_{23}\\F_{31}\\F_{32}\\F_{33}\end{bmatrix}=0 $$
$W$를 $N\geq8$의 상응점들로부터 유도된 위의 왼쪽 $N\times9$ matrix라고 하면, 이를
$$ W\text{f}=0 $$
라고 표현할 수 있다. ($\text{f}$는 fundamental matrix를 펴서 벡터화한 것)
실제로는 noise로 인한 영향을 줄여주기 때문에 8개보다 많은 correspondences를 이용해서 행렬 $W$를 만드는 게 좋다.
이 때, $W$를 SVD를 이용하면 추정되는 fundamental matrix $\hat{F}$ 를 구할 수 있다.
주의할 점은, 이렇게 구한 $\hat{F}$는 full rank인데, 실제 $F$는 rank가 2이다.
따라서, rank-2 approximation으로 SVD를 풀어야 한다.
위와 같은 조건을 만족하기 위해서는 다음과 같은 optimization problem을 풀면 된다.
$$ \underset{F}{\text{minimize}}\,\,\,\,\,\|F-\hat{F}\|_F\\\text{subject to}\,\,\,\,\det F=0 $$
이걸 SVD로 풀면, $\hat{F}=U\Sigma V^T$ 이고, best rank-2 approximation은 다음과 같다.
$$ F=U\begin{bmatrix}\Sigma_1&0&0\\0&\Sigma_2&0\\0&0&0\end{bmatrix}V^T $$
The Normalized Eight-Point Algorithm
실제로, 위와같은 standard한 Eight-Point Algorithm은 정확하지 않다.
그리고 점 $p_i$와 대응하는 epipolar line $\ell_i=Fp^\prime$ 과의 거리가 종종 매우 크다.
이러한 문제를 해결하기 위해 Normalized Eight-Point Algorithm을 사용한다.
기존의 eight point 알고리즘의 문제는 $W$가 SVD를 적용하기에 적절하지 않다는 것이다.
SVD가 잘 적용되려면, $W$가 0 혹은 0에 가까운 singular value를 하나 가지고 있어야 하고,
다른 singular value들은 0이 아니어야 한다.
하지만 $(1832,1023,1)$ 과 같이 현대 카메라는 픽셀 값이 매우 큰 경우가 많다.
$W$를 만들기 위해 주어진 점들이 상대적을 좁은 지역에 모여 있다면,
$p_i$와 $p_i^\prime$가 매우 유사할 것이고, 결과적으로 $W$가 매우 큰 singular value 하나와 상대적으로 작은 singular value들을 가지게 된다.
따라서 이러한 문제를 해결하기 위해 $W$에 다음의 두 가지를 만족하도록 전처리를 해주게 된다.
- 원점을 image의 center에 오도록 translation
- transformed된 점들과 원점과의 mean square distance는 2픽셀 ($\dfrac{2}{\text{mean distane}}$를 곱해줌)
Normalize를 해주게 되면 좌표는
$$ q_i=Tp_i\quad\quad q_i^\prime=T^\prime p_i^\prime $$
가 되고 이 좌표를 이용해서 fundamental matrix $F_q$를 구해주면 된다.
하지만 $F_q$는 normalize된 좌표의 fundamental matrix이므로 de-normalize를 해줘야한다.
따라서
$$ F=T^TF_qT^\prime $$
을 통해 $F$를 구하면 훨씬 real world에서도 적용이 잘 된다.
Image Rectification
Epipolar geometry에서 흥미로운 case가 나타날 때가 바로 두 이미지가 평행할 때이다.
두 이미지가 평행할 때, 먼저 essential matrix E를 계산해보자.
두 카메라가 같은 intrinsic matrix $K$를 갖고, 평행하므로 rotation도 없다고 생각할 수 있다.($R=I)$
이 경우, 특별히 $x$축을 따라서만 translation이 있다고 가정하면, $T=(T_x,0,0)$가 되고,
$$ E=[T_\times]R=\begin{bmatrix}0&0&0\\0&0&-T_x\\0&T_x&0\end{bmatrix} $$
로 유도할 수 있다.
$E$를 알았으므로, 이미지의 한 점에 대응하는 epipolar line의 방향도 찾을 수 있다.
점 $p^\prime$에 대응하는 epipolar line $\ell$의 direction은 다음과 같다.
$$ \ell=Ep^\prime=\begin{bmatrix}0&0&0\\0&0&-T_x\\0&T_x&0\end{bmatrix}\begin{bmatrix}u^\prime\\v^\prime\\1\end{bmatrix}=\begin{bmatrix}0\\-T_x\\T_xv^\prime\end{bmatrix} $$
이 경우, $\ell$이 수평(horizontal)한 직선임을 확인할 수 있다.
$\ell^\prime$도 같은 방식으로 계산해낼 수 있다.
Epipolar constraint $p^TEp^\prime=0$ 을 이용하면, $v=v^\prime$ 을 유도할 수 있는데,
이는 $p$와 $p^\prime$이 같은 $v-$좌표를 가짐을 의미한다.
따라서, rectification(주어진 두 image를 평행하게 만드는 작업)은 이미지의 대응점 간의 관계를 파악할 때 유용하다.
두 이미지를 rectifying할 때, 두 카메라 행렬 $K,K^\prime$ 또는 transformation 행렬 $R,T$를 몰라도 된다.
대신, 위에서 정리한 normalized eight point 알고리즘을 통해 구한 fundamental matrix를 이용하면 된다.
Fundamental matrix를 이용하면 대응점 $p_i,p_i^\prime$의 epipolar line인 $\ell_i^\prime,\ell_i$를 계산할 수 있다.
Epipole은 epipolar line들의 교점에 존재하기 때문에, epipolar lines set로부터 epipole $e,e^\prime$을 추정할 수 있다.
하지만 real world에서는 noise가 존재하므로, 모든 epipolar line들이 한 점에서 만나진 않는다.
따라서, epipole을 찾는 건 모든 epipolar line들에 제일 딱 맞는(least squared error을 minimizing하는) 점을 계산하는 것과 같다.
각 epipolar line은 $\{x|\ell^Tx=0\}$을 만족하는 vector $\ell$로 표현되므로, linear system of equation을 세워보면
$$ \begin{bmatrix}\ell_1^T\\\vdots\\\ell_n^T\end{bmatrix}e=0 $$
이 되고, 이를 SVD를 이용해서 epipole $e$를 찾으면 된다.
하지만 이렇게 epipole $e,e^\prime$을 찾고 나면, 이 epipole들이 수평선축의 무한대에 있지 않다는 것을 알 수 있다 (정의에 의하면 두 이미지가 평행하므로 무한대에 있어야 함, 그런데 noise때문에 실제로는 그렇게 안됨)
따라서, 이미지들을 parallel 하게 만들어주기 위해서 epipole $e$를 homography 변환을 통해서 수평선축의 무한대로 mapping해주어야 한다.

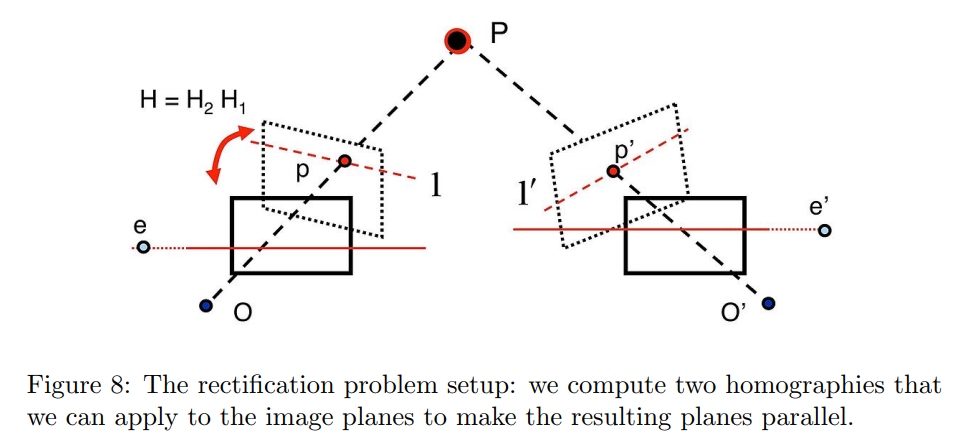
먼저 두 번째 epipole인 $e^\prime$을 horizontal axis의 무한대의 점 $(f,0,0)$로 mapping하기 위한 $H_2$를 찾아야 한다.
여러가지 가능한 homography가 있을 수 있지만, 가장 타당한 것을 찾아야 한다.
먼저, homography가 transformation 행렬과 같이 이미지 center근처의 점들에 rotation과 translation을 적용해야 한다.
그러기 위해서는, 먼저 두 번째 이미지를 homogeneous coordinate에서 center가 $(0,0,1)$이 되도록 translate 시킨다.
$$ T=\begin{bmatrix}1&0&-\frac{\text{width}}{2}\\0&1&-\frac{\text{height}}{2}\\0&0&1\end{bmatrix} $$
이와 같이 translation을 적용하고 나면, epipole이 horizontal axis위의 점 $(f,0,1)$이 되도록 회전을 해줘야 한다.
만약 평행이동한 epipole $Te^\prime$이 homogeneous coordinate $(e_1^\prime,e_2^\prime,1)$ 이 된다면, rotation matrix는
$$ R=\begin{bmatrix}\alpha\dfrac{e_1^\prime}{\sqrt{e_1^{\prime2}+e_2^{\prime2}}}&\alpha\dfrac{e_2^\prime}{\sqrt{e_1^{\prime2}+e_2^{\prime2}}}&0\\-\alpha\dfrac{e_2^\prime}{\sqrt{e_1^{\prime2}+e_2^{\prime2}}}&\alpha\dfrac{e_1^\prime}{\sqrt{e_1^{\prime2}+e_2^{\prime2}}}&0\\0&0&1\end{bmatrix}\quad\text{where}\quad\alpha=\begin{cases}1,&e_1^\prime\geq0\\-1,&\text{otherwise}\end{cases} $$
과 같다.
회전까지 해주고 나면, $(f,0,1)$을 수평선축의 무한대의 점 $(f,0,0)$으로 가져와야 하므로
$$ G=\begin{bmatrix}1&0&0\\0&1&0\\-\frac{1}{f}&0&1\end{bmatrix} $$
을 적용해준다.
그러면 마침내 무한대에 있는 epipole을 얻을 수 있다.
하지만 다시 regular image space로 가져와야 하므로 최종적으로 $H_2$는
$$ H_2=T^{-1}GRT $$
가 된다.
합리적인 $H_2$를 찾았으므로 first image의 matching homography $H_1$도 찾아줘야 한다.
$H_1$을 유도하는 과정은 범위를 벗어나므로 그냥 적어보자면,
$$ \underset{H_1}{\text{argmin}}\sum_i\|H_1p_i-H_2p_i^\prime\|^2 $$
$$ H_1=H_AH_2M $$
의 꼴을 갖고, ($F=[e]_\times M$)
$H_A$는
$$ H_A=\begin{bmatrix}a_1&a_2&a_3\\0&1&0\\0&0&1\end{bmatrix} $$
이다. ($a_1,a_2,a_3$는 뒤에서 추가 설명)
위의 식들이 갑작스럽게 느껴질 수 있다.
먼저 $M$이 무엇인지부터 알아야 한다.
$3\times3$의 skew-symmetric matrix $A$의 흥미로운 성질은, $A=A^3$ 이 성립한다는 것이다.
어떤 cross product matrix인 $[e]_\times$이건 skew-symmetric 이므로
$$ F=[e]\times M=[e]\times[e]\times[e]\times M=[e]\times[e]\times F $$
를 유도할 수 있다.
따라서
$$ M=[e]_\times F $$
이다.
만약 $M$의 column들이 $e$의 스칼라배만큼 더해진다해도, $F=[e]_\times M$은 여전히 up to scale이다.
따라서, $M$을 더 general하게 표현하면
$$ M=[e]_\times F+ev^T $$
이다. (실제로는, $v^T=\begin{bmatrix}1&1&1\end{bmatrix}$로 했을 때 제일 잘 됨)
그래서 결론적으로 $H_1$을 풀기 위해선, 위에서의 $\text{a}=(a_1,a_2,a_3)$를 찾아야 한다.
우리가 이제 $H_2$와 $M$을 알고 있으므로 $\hat{p_i}=H_2Mp_i$ 그리고 $\hat{p_i}^\prime=H_2p_i^\prime$ 이라 하면,
$$ \underset{H_A}{\text{argmin}}\sum_i\|H_A\hat{p_i}-\hat{p}^\prime_i\|^2 $$
가 된다.
더 나아가, $\hat{p_i}=(\hat{x_i},\hat{y_i},1)$, $\hat{p_i}^\prime=(\hat{x_i}^\prime,\hat{y_i}^\prime,1)$ 라고 하면, minimization problem 이 다음과 같이 바뀐다.
$$ \underset{\text{a}}{\text{argmin}}\sum_i(a_1\hat{x}_i+a_2\hat{y}_i+a_3-\hat{x_i}^\prime)^2+(\hat{y}_i-\hat{y_i}^\prime)^2 $$
$\hat{y}_i-\hat{y_i}^\prime$가 상수이므로, 더 간략하게 바꿔보면,
$$ \underset{\text{a}}{\text{argmin}}\sum_i(a_1\hat{x}_i+a_2\hat{y}_i+a_3-\hat{x_i}^\prime)^2 $$
가 된다.
$$ W=\begin{bmatrix}\hat{x}_1&\hat{y}_1&1\\&\vdots&\\\hat{x}_n&\hat{y}_n&1\end{bmatrix}\quad\quad b=\begin{bmatrix}\hat{x_1}^\prime\\\vdots\\\hat{x_n}^\prime\end{bmatrix} $$
라고 하면, 궁극적으로 $W\text{a}=b$ 꼴이 된다.
이렇게 $\text{a}$를 구하고 나면 $H_A$와 $H_1$도 구할 수 있다.
따라서, homography $H_1,H_2$를 위와 같은 과정을 거쳐 구해낸다.
Eight-Point Algorithm과 homography 구현 코드가 궁금하다면,
https://github.com/ianpark318/CS231A/blob/main/ps2/ps2_code/PSET2.ipynb 참고