Image filtering
What is Image?
- A grid (matrix) of intensity values (보통 0이 black, 255 : white를 의미)
- 이 map을 intensity(강도) map이라고도 함
- 이 grid를 pixel이라고 함
- 이 pixel 하나하나가 intensity value를 가지고 있음

Images as functions
이미지는 discrete한 pixel수를 가지고 있다.
- Pixel value
- grayscale/intensity
- [0, 255]
- color
- RGB는 [R, G, B] 즉 빨강 초록 파랑의 3 채널이고, 각각 [0, 255] per channel
- HSV [H, S, V]: Hue, saturation, value 로 나타낼 수도 있음
Image는 $R^2$에서 $R$ 또는 $R^M$ 으로의 함수 $f$라고 생각할 수도 있다.
- Grayscale 이라면 :
- $f(x,y)$는 각 위치 $(x,y)$의 intensity를 의미하며,
- Color 이면 :
- $f(x,y)=[r(x,y), g(x,y),b(x,y)]$ 의 $R^3$ 으로 매핑.

Image transformations
함수와 마찬가지로, 이미지에도 어떠한 operator를 적용할 수 있다.

그 중에서도 특별한 연산이 있는데, 합성곱 즉 convolution에 대해서 다뤄본다. (linear filtering)
Image denoising

그렇다면 images에서 noise가 나타나는 이유는 무엇인가?
- sensor noise
- Dead pixels
- Old photographs
- etc.,
그러면 Noise reduction은 어떻게 할 수 있을까?
- 근처의 pixel은 같은 object일 것이다.
- 따라서 비슷한 색깔을 가질 것이다.
- 각 픽셀을 주변 픽셀의 평균으로 대체한다.
Mean filtering
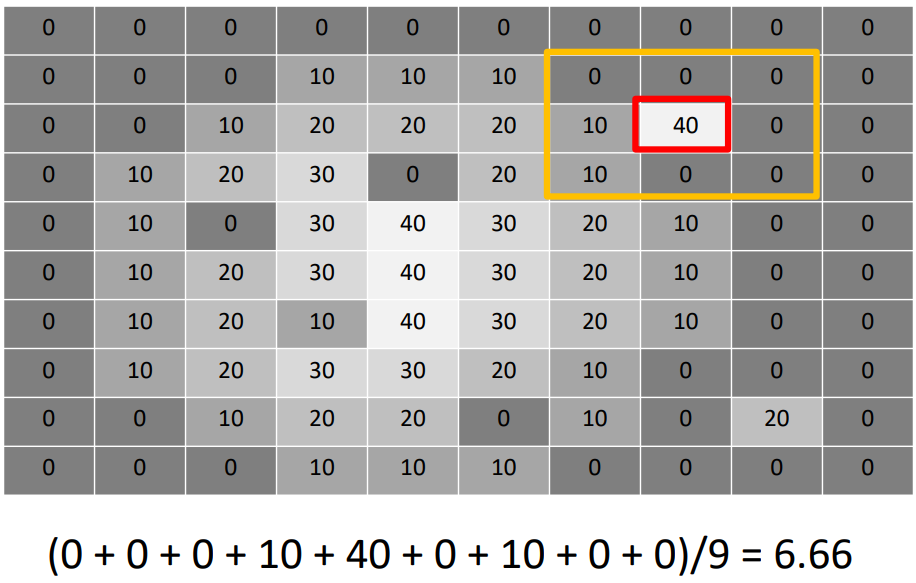
하지만 정수를 쓸 것이므로 7이 된다.
Kernel의 사이즈가 5가 되면?
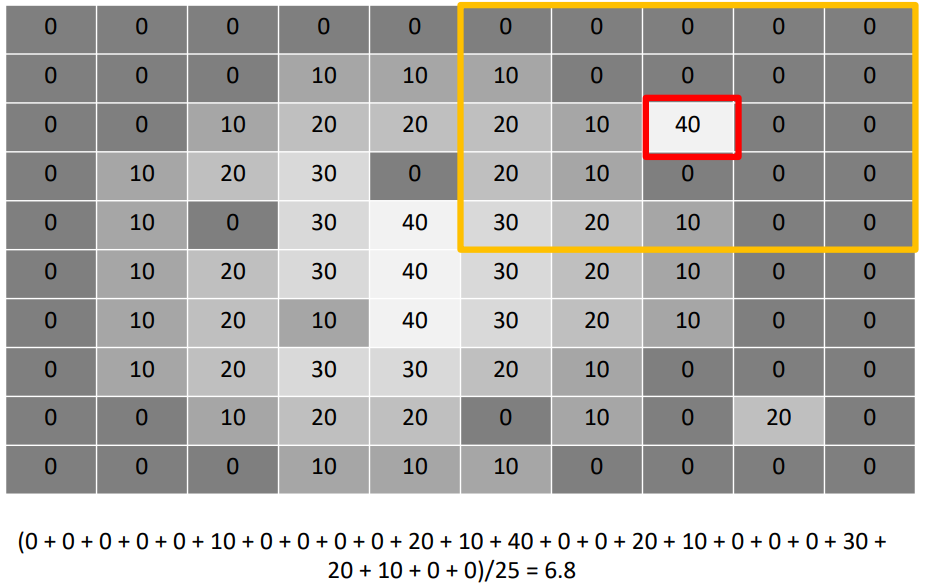
마찬가지로 7이다. (반올림)
Noise reduction using mean filtering

조금 부드러워지긴 했으나, 선명도가 떨어졌다. (sharpness)
Filters
- Filtering
- 각 픽셀들이 원래 이미지의 픽셀들의 linear combination이 되는 새로운 이미지를 생성하는 것이다.
- Why?
- 좀 더 유용한 information을 얻기 위해
- edge나 contour같은 특징을 추출
- image를 enhance하기 위해
- noise를 감소시키기 위해 blur 처리
- sharpen하기 위해
- CNN의 key 연산자이다.
- 좀 더 유용한 information을 얻기 위해
Linear filtering
가장 simple한 filtering의 종류: linear filtering (cross-correlation, convolution)
- 각 픽셀을 neighbor들의 linear combination으로 대체한다. (weighted sum)
아래와 같은 틀을 “kernel” 혹은 mask 또는 filter라고 한다.
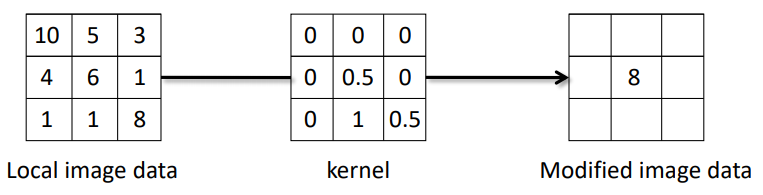
($10\times0+5\times0+3\times0+4\times0+6\times0.5+1\times0+1\times0+1\times1+8\times0.5=8$)
결국 mean filtering은 linear filtering의 일종이다.
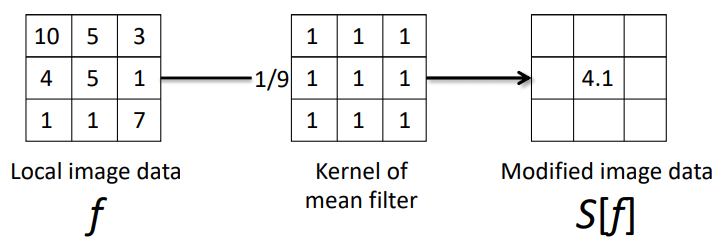
$$ Sf=\sum_{i=-1}^1\sum_{j=-1}^1\dfrac{f(m+i,n+j)}{9} $$
하지만 일반적인 linear filtering의 경우는 weight가 있다.
따라서
$$ Sf=\sum_{i=-1}^1\sum_{j=-1}^1w(i,j)f(m+i,n+j) $$
와 같이 되고, 이 때 $w(i,j)$가 kernel 또는 filter matrix의 각 원소가 된다.
그리고 kernel size가 달라질 수도 있다.
따라서 kernel size도 general하게 고려해주면,
$$ Sf=\sum_{i=-k}^k\sum_{j=-k}^kw(i,j)f(m+i,n+j) $$
가 된다. (kernel size는 $2k+1$)
Convolution and cross-correlation
Cross correlation
$$ S[f]=w\otimes f $$
$$ Sf=\sum_{i=-k}^k\sum_{j=-k}^kw(i,j)f(m+i,n+j) $$
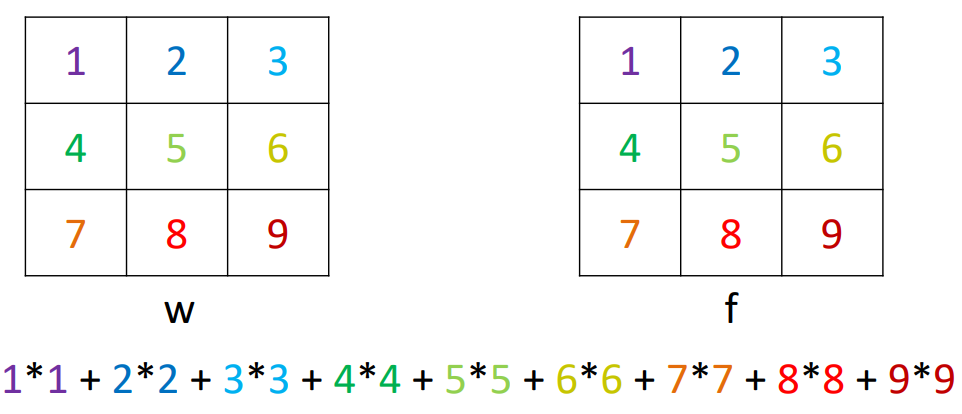
(즉 같은 자리에 대응하도록 곱해주고 더해주면 됨)
Convolution
$$ S[f]=w*f $$
$$ Sf=\sum_{i=-k}^k\sum_{j=-k}^kw(i,j)f(m-i,n-j) $$
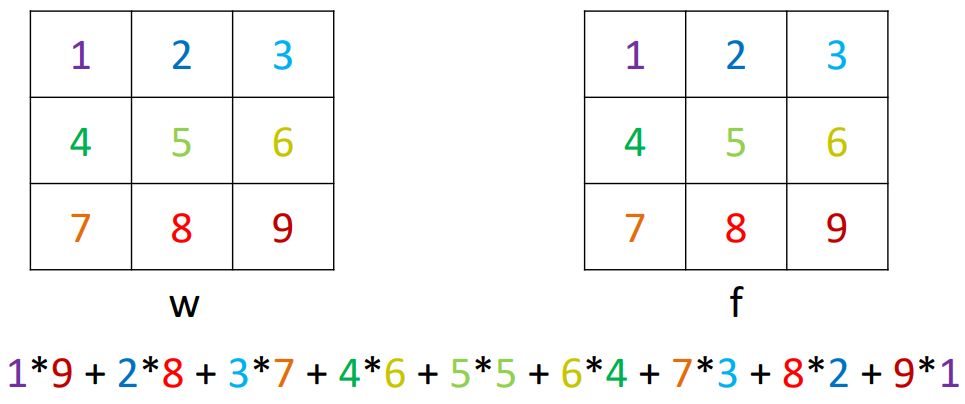
(행으로, 열로 커널을 각각 뒤집어서 cross-correlation을 하면 더 쉽다.)
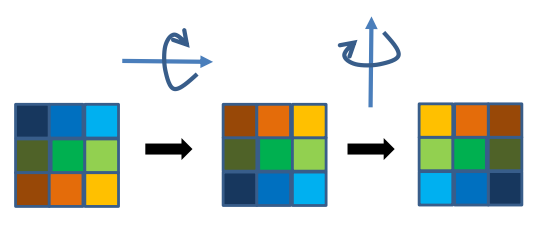
Cross-correlation과 convolution은 linearity를 만족한다.
또 다른 중요한 property로 Shift invariance가 있다.
shift가 일어나도 연산의 효과는 다르지 않음을 의미!!
그리고 shift하고 convolution을 하던지, convolution을 하고 shift를 하던 상관이 없음
Sharpening


Sharpening을 수식으로 나타내면 다음과 같다.
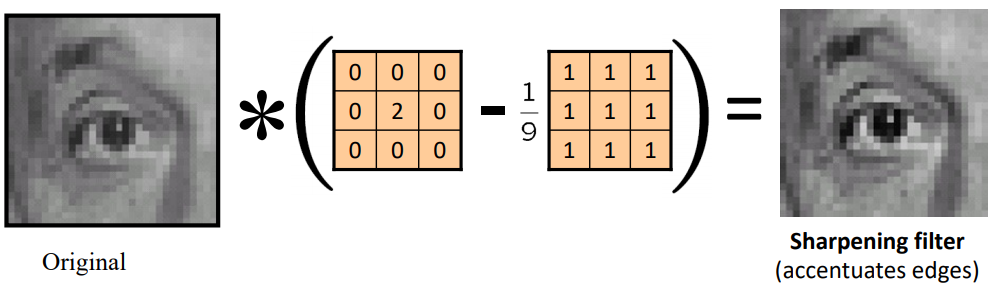
$$ \begin{align*}f_{sharp}&=f+\alpha(f-f_{blur})\\&=(1+\alpha)f-\alpha f_{blur}\\&=(1+\alpha)(wf)-\alpha(vf)\\&=((1+\alpha)w-\alpha v)f\end{align} $$
여기서 $f$는 원래 이미지를 의미하고,
$w,v$는 각각 다음과 같은 filter를 의미한다. (좌측부터 순서대로)
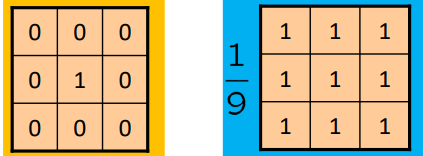
따라서 만약 \alpha=1 일 때, sharpening filter는 아래와 같다.
Gaussian filter
Mean filter와 달리, nearby pixel은 far-away pixel보다 더 correlated 할 것이라는 가정을 내포하는 filter이다.
따라서, nearby pixel에 더 weight를 많이 준다.
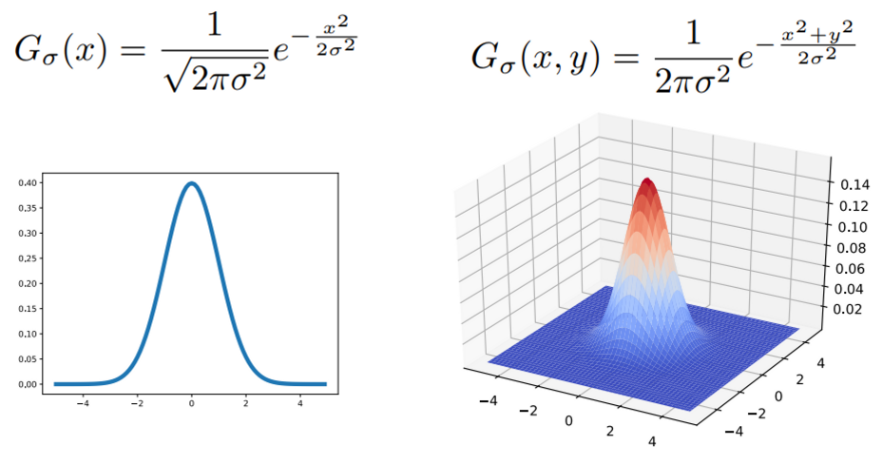
위의 그림은 독립변수가 1개, 2개일 경우의 gaussian distribution을 보여준다.
하지만, kernel은 이산적인 값을 가지기 때문에, 위의 continuous한 값을 가질 수 없다.
따라서, 이에 근사한 값을 가지도록 kernel을 구성해야 한다.
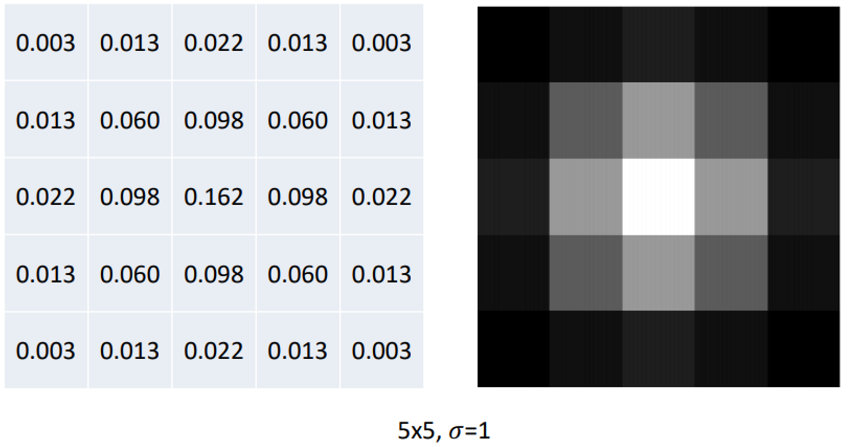
그리고 이처럼 kernel을 구성할 때, gaussian distribution의 앞 계수(factor)는 신경쓰지 않고 kernel의 모든 원소의 합이 1이 되도록 normalize만 해주면 된다.
다음은 gaussian filter를 이미지에 적용한 모습이다.

가우시안 필터는 “high-frequency” components를 제거하는 역할을 한다.
즉, low-pass filter 라고도 할 수 있다.
또한, gaussian filter끼리의 convolution의 결과도 gaussian이다.

(즉, $\sigma$의 gaussian kernel을 두 번 적용하는 것은 $\sigma\sqrt2$의 kernel을 한 번 적용하는 것과 결과가 같다.)
Non-linear filters
Thresholding

Thresholding은 필요한 임계값을 임의로 정하여 이미지를 처리하는 것으로, 이미지의 전, 후처리에서 중요한 filter중 하나이다.
$$ g(m,n)=\begin{cases}&255, \quad &f(m,n)>A\\&0&otherwise\end{cases} $$
Rectification
$$ g(m,n)=\max(f(m,n),0) $$
Rectification은 convolutional network의 중요한 component중 하나이다.
(특히 ReLU)
Median filter
Mean은 outlier에 굉장히 민감하게 반응한다.

따라서, mean filtering이 잘 적용이 되지 않는다.
따라서, median(중간값)을 택하여 해당 pixel에 replace해준다.
다음과 같이 speckle noise를 이와 같은 방법으로 처리할 수 있다.
