Edge detection
Edge detection
Edge detection이란 뭘까?

Edge detection은 2D image를 curve의 set으로 변환하는 것이다.
즉, 해당 scene 또는 object의 가장 두드러지고 핵심적인 feature를 추출하는 것이라고 할 수 있다.
그렇다면 왜 edge를 사용하는 걸까?
왜냐하면 edge는 빛과 색깔에 비교적 robust하기 때문이다.

즉, 위와 같이 색깔이 다른 같은 모델의 자동차는 비슷한 edge feature를 가지고 있을 것이다.
따라서 edge는 recognition과 이미지의 patch들을 matching하는 데 유용하게 쓸 수 있다.
그렇다면 edge에 대해서 조금 고민해보자.

Edge는 위의 그림과 같이 단순히 하나의 이유만으로 생기는 것이 아니다.
깊이가 달라서, 색깔이 달라서, 조명이 달라서 등등 여러 원인에 의해 생길 수 있는 것이 바로 edge이다.
앞서 image filtering에서 우리는 image를 function으로 생각할 수 있다고 했었다.

위의 그림과 같이, edge는 steep cliffs(가파른 절벽)처럼 보인다.
이렇듯 intensity의 값이 확 바뀌는 부분을 우리는 edge라고 생각해 볼 수 있다.
Characterizing edges
앞서 말했듯, edge는 image intensity function의 값이 급격하게 바뀌는 부분이라고 할 수 있다.

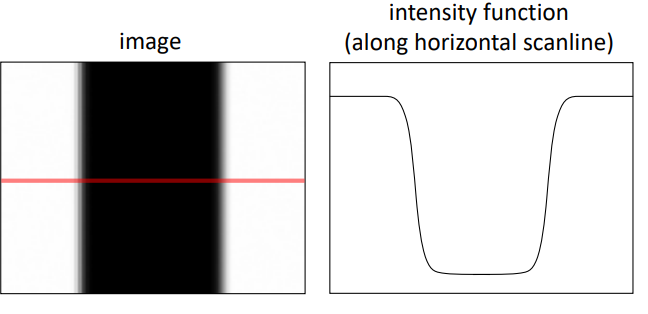
제일 좌측 그림을 본래 image라고 한다면, intensity는 중간 그림처럼 해당 부분에서(horizontal 방향을 따라) 아래로 급격히 떨어졌다가 다시 오르는 형태를 띄게 된다.
즉, 이 intensity function을 미분해보면, 우측 그림처럼 미분의 값이 가장 extreme한 곳(극값)이 edge라고 할 수 있을 것이다.
Image derivatives
하지만 여기서 하나 문제점이 발생하는데,
image intensity function의 정의역은 discrete하며, 어떤 특정한 수학적인 함수로 정의할 수 없기 때문에, 미분을 어떻게 해주어야 할지 고민할 수 밖에 없다.
그렇다면, 이 digital image $F[x,y]$를 어떻게 differentiate할까?
물론, 이 digital image를다시 continuous한 image 로 바꿔서 미분을 해볼 수도 있겠으나,
discrete derivative를 적용하는 방법이 더 간단하고 직관적이다. (finite difference)
$$ \dfrac{\partial f}{\partial x}[x,y]\approx F[x+1,y]-F[x,y] $$
즉 위의 식처럼 $x$방향으로 1만큼 옆에 있는 픽셀과의 pixel intensity차이를 이용하는 것이다.
그럼 이렇게 구현한 linear filter은 아래와 같이 이루어진다. (비어있는 칸 0)
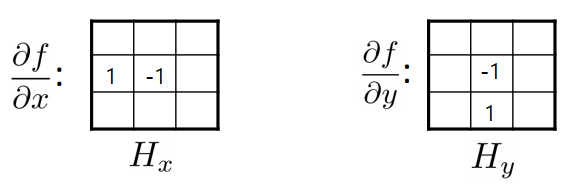
그런데 이 filter를 적용하면 $F[x-1,y]-F[x,y]$ 가 되지 않느냐고 헷갈릴 수도 있지만,
convolution 연산을 적용하는 것이기 때문에, $F[x+1,y]-F[x,y]$ 이 된다.
마찬가지로 $y$축 방향은
$$ \dfrac{\partial f}{\partial x}[x,y]\approx F[x,y+1]-F[x,y] $$
가 된다.
Image gradient
$x,y$축으로의 미세한 이산적인 차이를 이용해 derivative를 구했으므로, 이제 image의 gradient를 정의해볼 수 있다.
이미지의 gradient는 다음과 같이 나타난다.
$$ \nabla f=\bigg[\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y}\bigg] $$
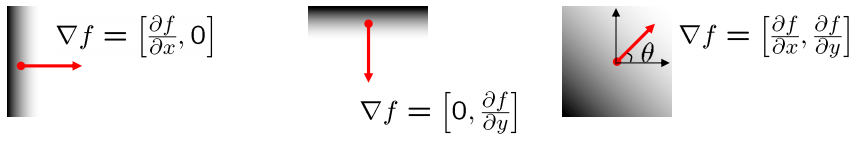
Gradient는 해당 픽셀 위치에서, 가장 급격하게 intensity가 증가하는 방향을 가리키게 된다.
따라서, 급격하게 변할수록 이렇게 intensity가 급격하게 변할수록 edge일 가능성이 크다고 말할 수 있으며,
edge strength는 gradient의 magnitude와 같게 된다.
$$ \|\nabla f\|=\sqrt{\bigg(\dfrac{\partial f}{\partial x}\bigg)^2+\bigg(\dfrac{\partial f}{\partial y}\bigg)^2} $$
또한, gradient의 direction은 다음과 같이 얻을 수 있다.
$$ \theta=\tan^{-1}\bigg(\dfrac{\partial f}{\partial y}\bigg/\dfrac{\partial f}{\partial x}\bigg)=\tan^{-1}\bigg(\dfrac{\partial x}{\partial y}\bigg) $$

Effects of noise
하지만 일반적으로 아래와 같은 그림처럼 noise 없이 깔끔하게 intensity가 변화하지는 않는다.
이미지란 본래 noise를 가지고 있기 마련이며, 그 결과는 보통 아래처럼 나타난다.
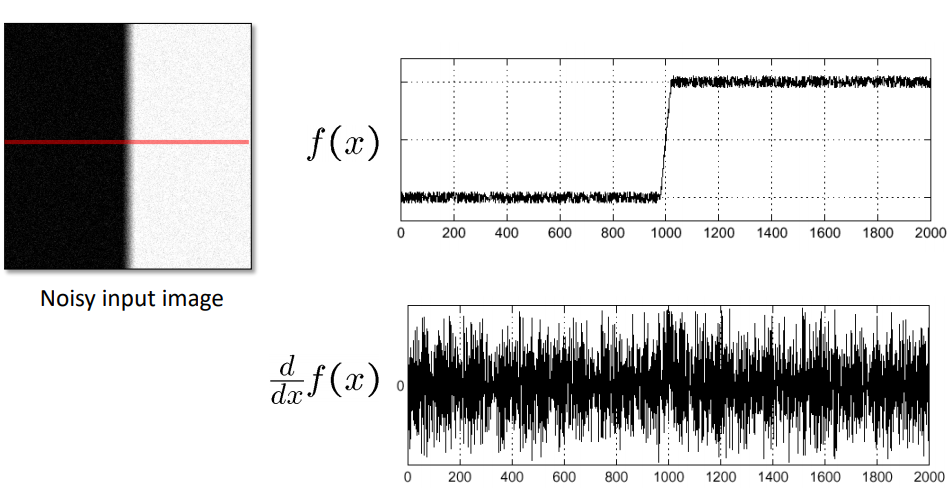
이처럼 noise가 있을 경우에는 미분을 해서 극값을 이용해 edge를 찾는 게 매우 challenging하다.
이런 noise문제를 어떻게 해결하면 좋을까?
Solution: smooth first
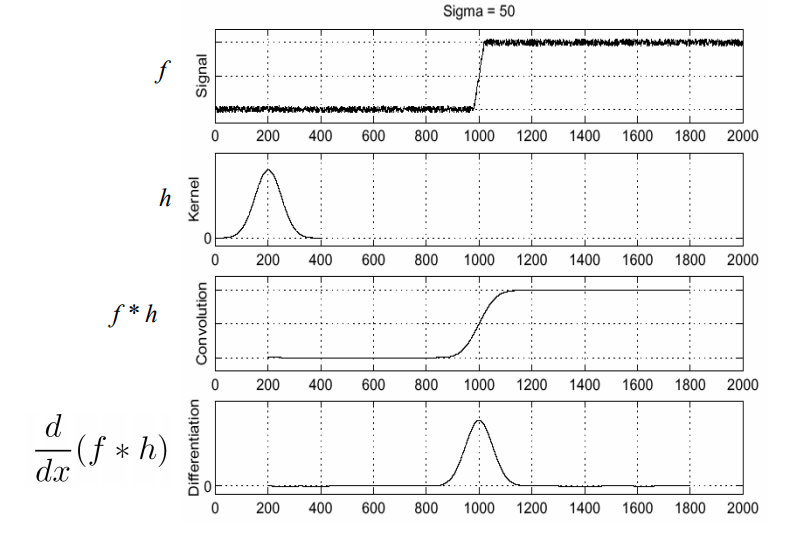
앞서 우리는 gaussian filter에 대해서 배웠다.
Gaussian filter는 low-frequency는 통과시키며, high-frequency는 무시해버리는 low-pass filter라고 했었다.
따라서, noise가 있는 intensity function에 gaussian filter를 적용하면 세 번째 줄의 그래프처럼 상당히 smooth한 function을 얻을 수 있다.
그 후, 우리가 목표했던 방식으로 edge를 찾아나가면 된다.
즉, $\dfrac{d}{dx}(f*h)$ 의 극값을 찾는다.
Associative property of convolution
Discrete한 pixel에 대한 differentiation을 convolution 연산을 통해 해주었는데, convolution 연산은 associative 하다.
따라서,
$$ \dfrac{d}{dx}(fh)=f\dfrac{d}{dx}h $$
이 성립한다.
어차피 같은 결과를 얻는다면, 연산량을 줄이는 것이 바람직하므로 오른쪽 $f*\dfrac{d}{dx}h$ 처럼 gaussian kernel을 먼저 미분해주고, 그 결과와 이미지를 convolution한다.
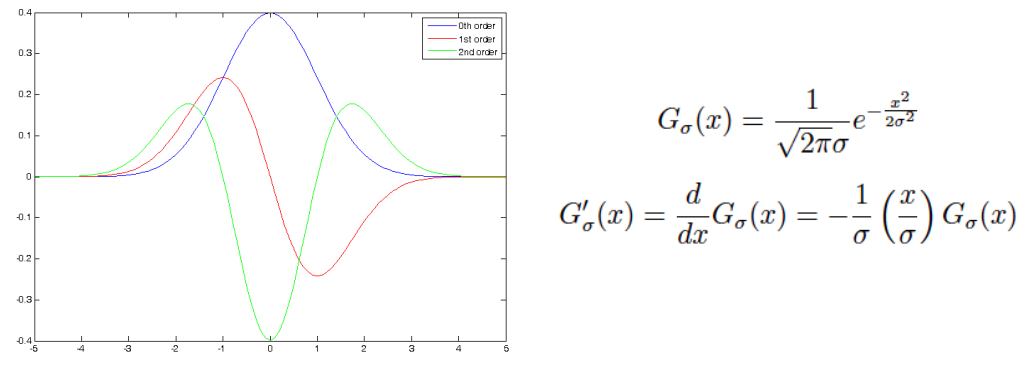
The 1D Gaussian and its derivatives
독립변수가 하나인 gaussian distribution의 경우 미분의 결과는 아래와 같다.
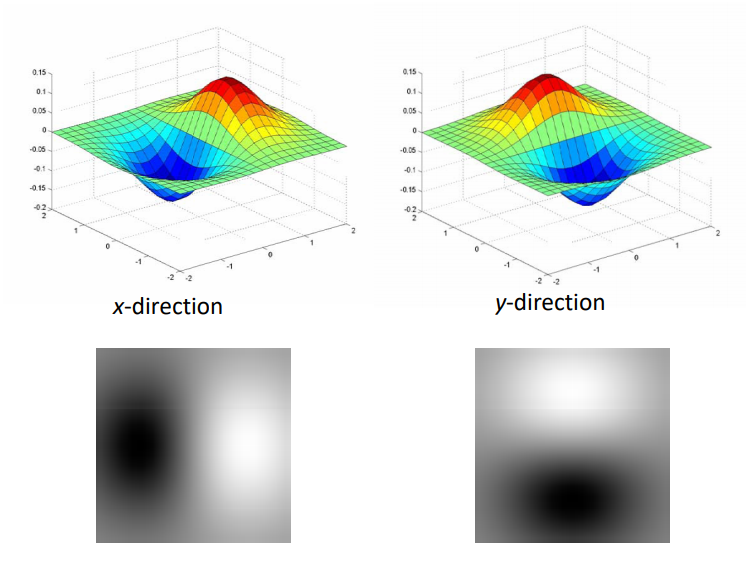
2D edge detection filters
하지만 우리는 독립변수가 $x,y$ 두 개인 경우를 고려하므로, 각 변수(축)에 대해 각각 따로 미분을 고려해주어야 한다
따라서, $x, y$축에 대한 2D gaussian distribution의 미분 결과는 아래와 같다.
The Sobel operator
위의 그림에서 $x,y$ direction에서의 미분 결과를 살펴보았는데, 이를 kernel로 나타내면, 다음과 같다.
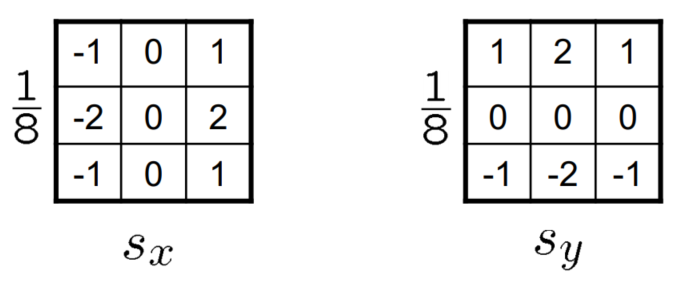
위 그림처럼, 정확한 gradient magnitude를 알고 싶다면, $\dfrac{1}{8}$ term을 넣어주어야 한다.
(하지만 그냥 gradient를 이용해서 edge를 detect하기 위함이면 없어도 된다.)
또 하나 중요한 것은, 나도 헷갈렸던 건데, $x,y$ 축과 필터의 방향을 잘 맞춰야 한다는 것이다.
위의 필터는 이미지를 아래의 축을 기준으로 생각한 결과이다.
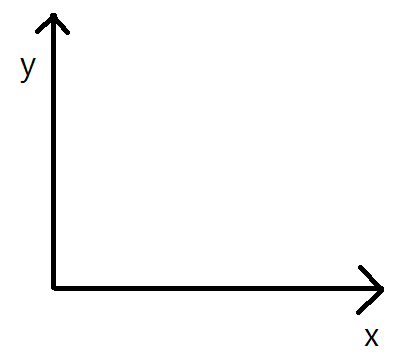
하지만, numpy 행렬이나 이미지와 같이 좌측 상단이 원점인
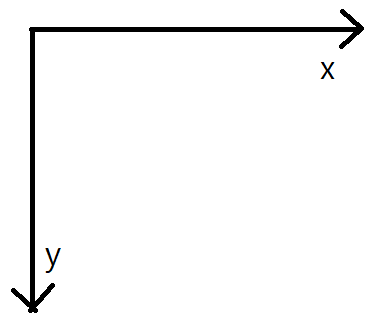
위와 같은 경우를 생각해보면, x filter는 그대로이지만, y filter의 방향을 바꿔야 한다.
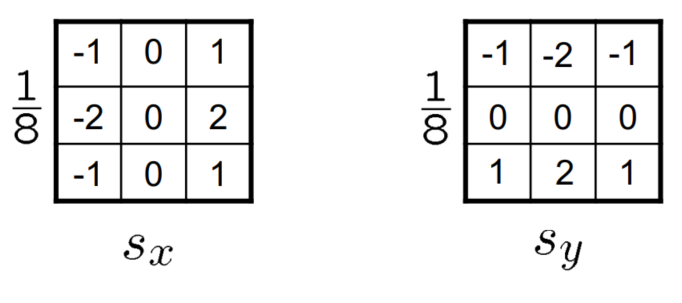
따라서 위와 같은 filter 를 가져야 한다.
(Convolution 연산을 적용할 것이라면 filter를 x, y축으로 반전시켜야 하지만, 실질적으로 이건 후에 180도 반대인 것과 똑같은 동작을 하므로 큰 의미를 가지지 못함. 따라서 상관 없다고 말할 수 있다.)
다음은, sobel operator를 적용한 예이다.

Gaussian filter을 이용해서 noise를 줄여주는 것은 매우 바람직하지만, 그 결과로 edge가 좀 두껍게 detecting되는 문제가 생긴다.
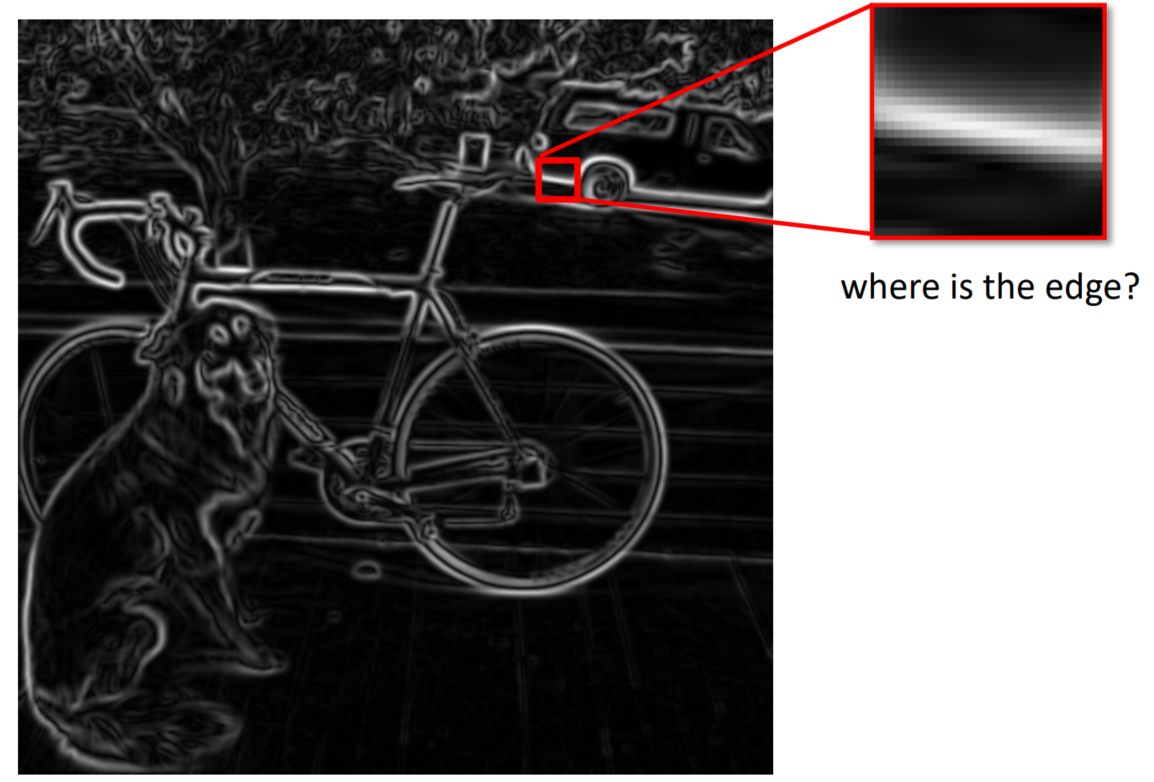
우리는 얇은 edge에 관심이 있으므로 두꺼워진 이 edge를 다시 얇게 하는 작업이 필요하다.
Non-maximum supression

Sobel operator로 얻은 $x,y$축에 대한 값을 arctan를 이용해 각 $\theta$를 구한다.
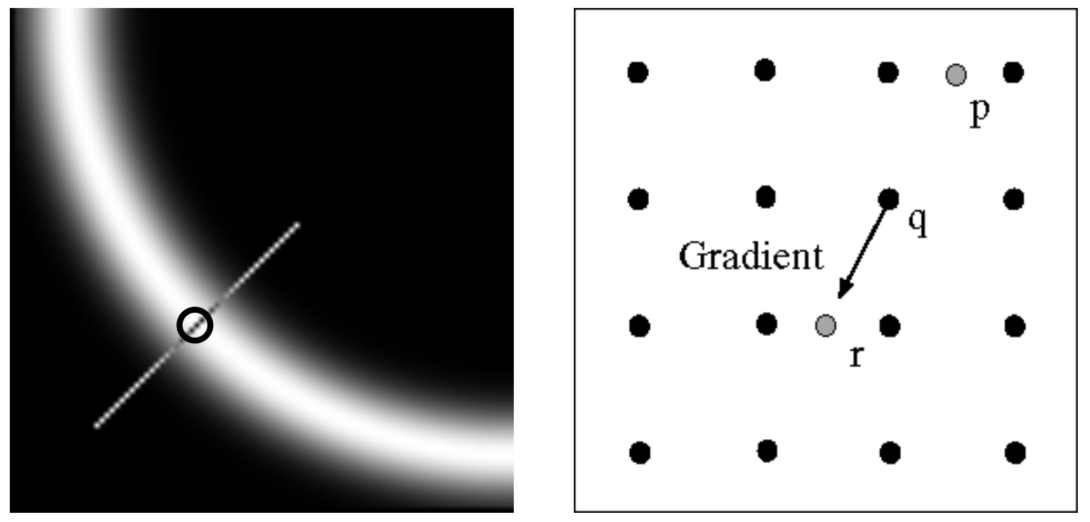
$\theta$를 이용해서, 해당 gradient의 방향(해당 방향과 반대방향 포함)으로 non maximum suppression을 진행해준다.
여기서 non maximum suppression이란, 해당 pixel이 gradient의 양방향에 있는 pixel보다 커야만 그대로 두고, 아닌 경우 0으로 아예 죽여(?)버리는 기법을 의미한다.
따라서, 해당 gradient 방향으로 가장 큰 값만 남기게 되므로, thin한 edge가 형성될 수 있다.
(그런데 이 non maximum suppression의 구현 과정에서도, 매우 헷갈리는 상황이 발생하는데, 이후 구현 관련 포스팅에서 다뤄보도록 한다.)
하지만, NMS를 보통은 [0, 45, 90, 135]의 네 방향에 대해서만 적용하는데, 따라서 해당 각도들이 아닌 각도들을 [0, 45, 90, 135]의 방향으로 interpolating해주는 작업이 필요하다.
이 경우, $\pm22.5$도만큼의 범위를 정해놓고 interpolating을 해주면 된다.
다음은 NMS를 적용하기 전과 후의 이미지이다.

Thresholding edges
이제 최종적으로 edge를 detecting 하기 위해서, strong한 edge들만을 남겨놓고 싶다.
이 때, 2개의 threshold를 사용하며, 큰 threshold $T$와 작은 threshold $t$ 를 사용한다.
- $R > T$ 인 경우 : strong edge
- $t < R < T$ 인 경우 : weak edge
- $R < t$ 인 경우 : no edge
이렇게 분류된 pixel들은 다음과 같이 처리한다.
- Strong edge로 분류된 pixel : 그대로 남겨둔다.
- Weak edge로 분류된 pixel : strong edge와 연결되어 있다면(주위 8 pixel중 하나에) strong edge가 된다. (없으면 no edge)
- No edge : 그냥 edge 없는 경우.

정리해보면, canny edge detector는 다음과 같은 algorithm으로 구성된다.

Canny edge detector는 여러 parameter로 조정을 할 수 있는데, 그 중 $\sigma$에 대해 다뤄보자면, $\sigma$는 gaussian blurring의 width를 조정한다고 할 수 있다.
- large $\sigma$ : “large-scale” edge를 detect함.
- small $\sigma$ : fine edge를 detect함.
