저번 시간에 이어 Data Wrangling에 대해서 다뤄볼텐데, 그 전에 outlier란 무엇이고 어떻게 처리하는지 알아보도록 하자.
Outlier
An outlier is an observation that lies an abnormal distance from other values in a random sample from a population. In a sense this definition leaves it up to the analyst to decide what will be considered abnormal.
'이상치'라고 하는 이 outlier는 다른 값들에 비해 비정상적인 값을 갖는데, data wrangling 과정에서 analyst는 이 '비정상'적인 값의 범위를 임의로 판단하여 outlier를 판단할 수 있다. (그 분석에 의해 dataset과 model의 accuracy가 더 향상된다면)
하지만 통상적으로는 outlier를 Q1-1.5*IQR 보다 작거나 Q3+1.5*IQR보다 큰 경우를 말한다.
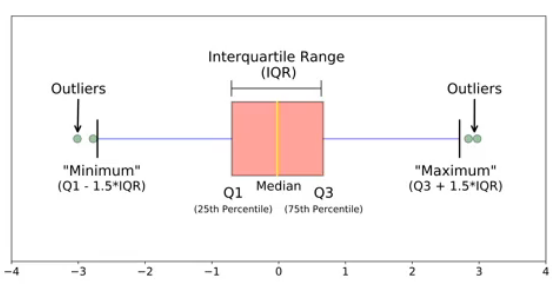
EDA과정에서 Boxplot을 그리면 쉽게 찾을 수 있다.
또한 Standardization을 통해서도 찾을 수 있다.(일변량의 경우)
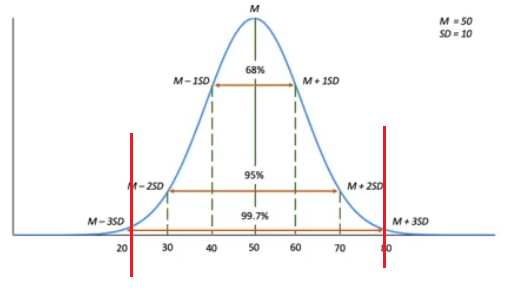
M + 3SD 보다 크거나, M - 3SD 보다 작을 때 이를 이상치로 정의하기도 한다.
이제 코드를 통해 outlier를 어떻게 처리하는지 알아보자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(5)
n_samples = 1000
height = 4*np.random.randn(n_samples).round(2) + 170
weight = 5*np.random.randn(n_samples).round(2) + 65
df_raw = pd.DataFrame({"height": height, "weight": weight})
# copying data
df = df_raw.copy()
height_1 = height.copy()
height_1[0] = 200
df["height_1"] = height_1이상치를 넣어준 height_1 이라는 feature에 대한 일변량 이상치를 생각해보자.
f = sns.boxplot(x = df.height_1)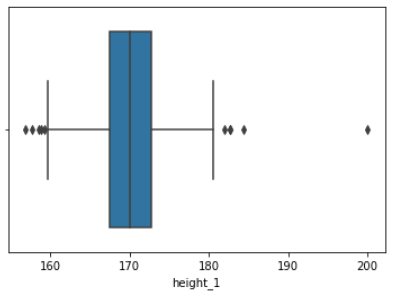
boxplot을 그려보니 넣어줬던 200을 가지는 outlier가 잘 드러난다.
Q1 = df.height_1.quantile(0.25)
Q3 = df.height_1.quantile(0.75)
IQR = Q3 - Q1
lower = Q1 - 1.5*IQR
upper = Q3 + 1.5*IQR
print(lower, upper)
# 159.58500000000004 180.745Q1, Q3와 lower, upper bound를 정해준다.
# filter using query
filtered = df.query('@lower <= height_1 <= @upper')
f = sns.boxplot(x = filtered.height_1)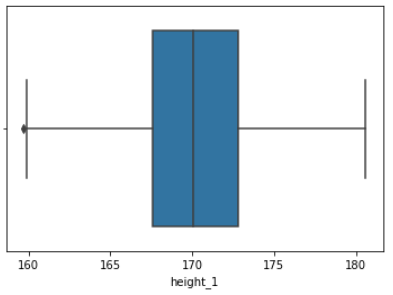
data에 query문에 조건을 줌으로써 아웃라이어에 해당하는 값들은 삭제가 된다.
Boxplot으로도 이상치가 제거된 것을 볼 수 있다.
다만 왼쪽에 하나 있는 이상치는 query문에 조건으로 filter 되고 난 후 나머지 데이터들에 의해 이상치로 구분된 데이터이다.
또 다른 방법으로 query 대신 loc을 이용할 수도 있다.
# filter using loc
df2 = df.copy()
df2.loc[df2.height_1 > upper] = np.nan
df2.loc[df2.height_1 < lower] = np.nan
df2 = df2.dropna()
f = sns.boxplot(x = df2.height_1)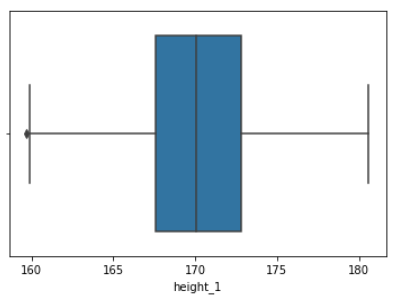
또 아까 살펴봤듯이, 표준편차를 이용해 이상치를 정의할 수도 있다.
# filter using SD
df3 = df.copy()
df3 = df3.query('-3 <= h_sc <= 3')
f = sns.boxplot(x = df3.height_1)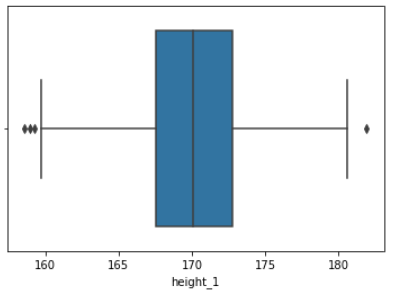
이러한 보편적인 정의에 의한 이상치는 분석하는 이가 참고하기 위한 자료로 사용할 수 있으며, 위에서 설명했듯이 데이터나 모델의 정확성 개선을 위해 이상치를 분석자 임의로 정할 수 있다는 것에 유의하자.
Data Encoding
Data encoding에는
1. 연속적인(continuous, numerical) 값을 categorical(nominal)한 값으로 바꿔주거나 (ex. 점수를 등급으로)
2. categorical한 값을 numerical한 값 또는 set of binary variable로 바꿔주는
경우가 있다.
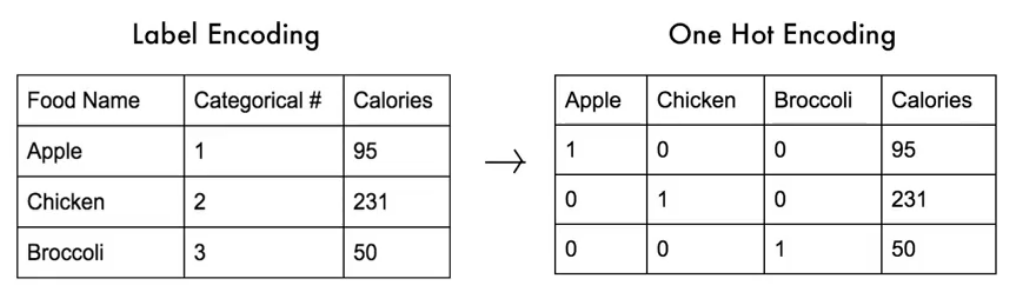
코드로 살펴보자.
df.loc[df.h_sc > 1, 'group'] = 'tall'
df.loc[(df.h_sc <= 1) & (df.h_sc >= -1), 'group'] = 'normal'
df.loc[df.h_sc < -1, 'group'] = 'small'
df[:10]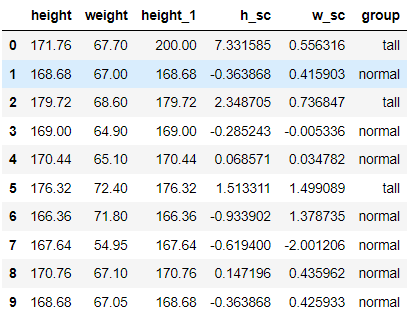
표준편차를 이용해 표준편차가 [-1,1]이면 normal, 1보다 크면 tall, 1보다 작으면 small 로 분류했다.
이제 이를 label encoding 해보자.
# label encoding
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
df['en'] = encoder.fit_transform(df.group)
encoder.classes_
# array(['normal', 'small', 'tall'], dtype=object)사이킷런의 preprocess에 LabelEncoder를 이용해 해당 categorical 한 (normal, small, tall)을 0, 1, 2 로 라벨링해준다.
라벨링된 데이터를 이용해 one hot encoding 을 해보자.
# one-hot encoding
df_group = pd.get_dummies(df.group)
df_group.head()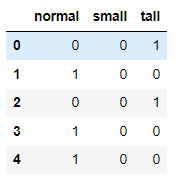
이렇게 여러가지 encoding 기법과 outlier를 다루는 방법에 대해서 알아보았다.
3번의 포스팅에 나눠 Data Wrangling에 관해 정리하면서, 아주 기본적인 것이지만 데이터의 전처리 과정에 대한 중요성과 방법에 대해 알 수 있었다.
//문제제기 및 피드백 언제든지 감사히 받겠습니다.
'Computer Science > DL || ML' 카테고리의 다른 글
| Data wrangling #2 - Data Scaling (0) | 2022.06.06 |
|---|---|
| Data wrangling #1 - Data Cleaning (0) | 2022.06.06 |
| [ML] KNN(k-Nearest Neighbor) (0) | 2022.05.07 |
| [ML] 선형회귀(Linear Regression) (0) | 2022.04.29 |
