Vanishing Points and Lines
지금까지는 2D 에서 무한대에서의 직선과 점을 다뤘다면 이제 이를 3D 에도 적용시켜본다.
3D에서는 평면의 개념을 도입해야한다.
평면을 vector로 $\begin{bmatrix}a & b & c & d\end{bmatrix}^T$로 표현 가능하고,
여기서 $(a,b,c)$는 법선벡터(normal vector)를 의미하며 $d$는 법선벡터 방향으로 원점에서 평면까지의 거리이다.
Formal하게 평면을 정의해보면 다음과 같다.
$$ x^T\begin{bmatrix}a\\b\\c\\d\end{bmatrix}=ax_1+bx_2+cx_3+d=0 $$
3D 에서 직선이란 두 평면의 intersection으로써 정의된다.
자유도가 4이기 때문에(? 모르겠다), 3D 공간상에서 표현하기가 쉽지 않다.

Points는 3D에서도 2D에서와 비슷하게 정의된다.
3D에서의 points at infinity도 parallel line들의 intersection point로 정의된다.
게다가, 이 points at infinity $x_\infty$중의 한 점에 projective transformation을 적용하면,
더 이상 무한대의 점이 아닌, image plane의 point $p_\infty$를 얻을 수 있다.(homogeneous coordinate)
이 때, 이 점 $p_\infty$를 vanishing point라고 부른다.
그렇다면 이 vanishing point로 뭘 할 수 있는지가 중요하다.
3D 상의 평행한 직선들을 통해서 이 평행한 직선들의 vanishing point와 camera parameter인 $K,R,T$ 를 도출해낼 수 있다.
$d=(a,b,c)$를 camera reference system에서 3D parallel line들의 direction으로 정의하자.
알고있다시피 이 직선들은 point at infinity에서 만나게 되고, 이 점을 image로 projection한 결과는 vanishing point $v$ 가 될 것이다.
$$ v=Kd $$
위 식이 어떻게 나왔는지 살펴보면,
앞서 아래와 같은 식을 챕터1에서 배웠었다.
$$ P^\prime=MP=K\,[I\quad0]\,P $$
(camera reference system에서의 3D parallel line이므로 rotation, transition 해당 없음)
따라서 $x_\infty$에 intrinsic camera matrix $M$을 적용하면 아래와 같이 유도를 할 수 있다.
$$ v=Mx_\infty=K\begin{bmatrix}I&0\end{bmatrix}\begin{bmatrix}a\\b\\c\\0\end{bmatrix}=K\begin{bmatrix}a\\b\\c\end{bmatrix}=Kd $$
역으로, direction 벡터 $d$를 얻기 위해선,
$$ d=\frac{K^{-1}v}{\|K^{-1}v\|} $$
와 같이 크기가 1이 되도록 normalize를 해주면 된다. (근데 왜 굳이 normalize 해주는 거지?)
평면 $\Pi$를 평행한 직선들의 superset이라고 해보자.
그렇다면 각 parallel lines set은 point at infinity에서 만난다.
그리고 그 points at infinity들을 지나는 직선을 $\Pi$에 대한 line at infinity $\ell_\infty$라고 한다.
(Line at infinity는 이 점들을 지나는 직선 뿐만 아니라, 두 평행한 평면의 intersect로도 정의가능하다.)
$\ell_\infty$에 image plane으로의 projective transformation을 적용하면 이 직선은 더 이상 무한에 있는 직선이 아니라 vanishing line 또는 horizon line $\ell_{\text{horiz}}$ 라고 부른다.
Horizon line은 이미지에 있는 상응하는 vanishing point들을 지나는 직선이기도 하며,
다음과 같이 계산할 수 있다.
$$ \ell_{\text{horiz}}=H_P^{-T}\ell_\infty $$
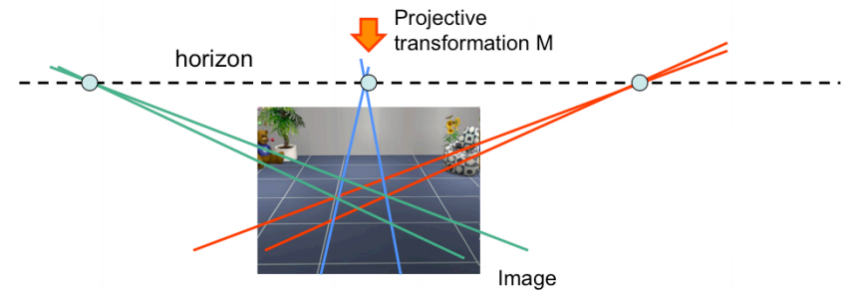
이런 horizon line 개념은 위 그림처럼 수학적으로는 평행하지 않아보이는 직선을 3D 세계에서는 평행하다고 추론할 수 있게 해준다.
더 나아가, 3D의 평면의 법선 $n$과, 이미지 내의 상응하는 horizon line $\ell_{\text{horiz}}$간의 흥미로운 관계를 도출해낼 수 있다.
$$ n=K^T\ell_{\text{horiz}} $$
이 말인 즉슨, 우리가 3D의 평면과 연관된 horizon line을 알 수 있고, 카메라가 calibrate 되어있다면,
해당 평면의 방향을 알 수 있음을 의미한다.
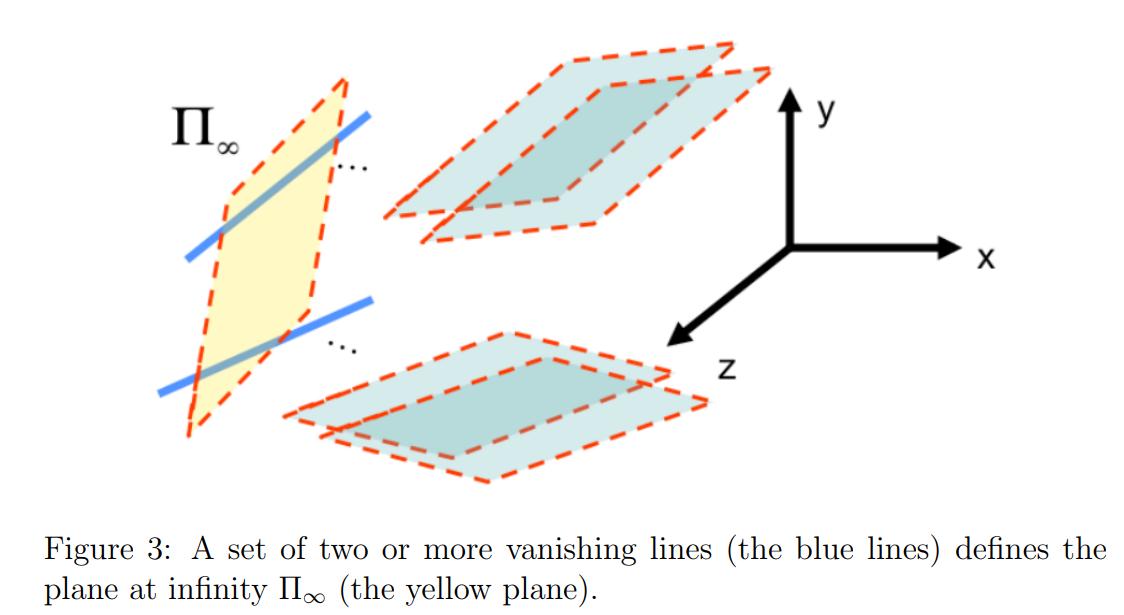
또 새로운 개념이 등장하는데, 직선에서 더 확장된 무한에 있는 평면인 plane at infinity $\Pi_\infty$이다.
이 평면은 2개 이상의 vanishing line으로 정의될 수 있으며,
homogeneous coordinates으로 vector $\begin{bmatrix}0&0&0&1\end{bmatrix}^T$로 표현된다.
마지막으로 소개할 성질은 3D 상의 직선과 평면, 그리고 image plane에서 상응하는 vanishing points와 lines와 관련된 것이다.
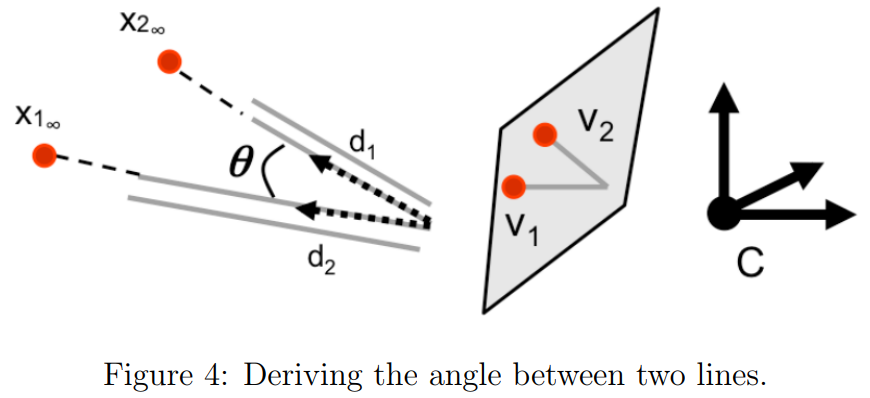
3D상의 두 쌍의 평행한 직선의 direction이 $d_1,d_2$이고 각각의 교점(points at infinity)이 $x_{1,\infty},x_{2,\infty}$ 라고 하자.
그리고 $v_1,v_2$이 그에 상응하는 vanishing point라고 했을 때, $d_1,d_2$가 이루는 각 $\theta$는 다음과 같다.
$$ \cos\theta=\frac{d_1\cdot d_2}{\|d_1\|\|d_2\|}=\frac{v_1^T\omega v_2}{\sqrt{v_1^T\omega v_1}\sqrt{v_2^T\omega v_2}},\quad \text{where}\,\,\,\omega=(KK^T)^{-1} $$
이를 3D의 평면으로 확장해서 생각해볼 수도 있다.
먼저, 어떠한 평면이든 평면으로 만들어낼 수 있는 vanishing line $\ell_{\text{horiz}}$와 법선 $K^T\ell_{\text{horiz}}$를 구해낼 수 있다는 것을 기억해두자.
따라서, 두 평면의 법선벡터 $n_1,n_2$를 통해 두 평면이 이루는 각 $\theta$를 구할 수 있다.
$$ \cos\theta=\frac{n_1\cdot n_2}{\|n_1\|\|n_2\|}=\frac{\ell_1^T\omega^{-1} \ell_2}{\sqrt{\ell_1^T\omega^{-1} \ell_1}\sqrt{\ell_2^T\omega^{-1} \ell_2}},\quad \text{where}\,\,\,\omega=(KK^T)^{-1} $$
A Single View Metrology Example

우리가 이미지에 있는 두 평면을 3D world에서 식별할 수 있다고 해보자.
(예를 들어 위의 사진에서 건물의 두 벽면이 plane이라고 식별할 수 있다면)
그렇다면 앞서 배웠듯이 위의 사진처럼 두 vanishing point $v_1,v_2$를 계산할 수 있다.
그리고 두 평면(사진에서는 벽면)이 수직으로 만난다는 것또한 알고 있다면,
parallel한 두 쌍의 직선을 그린 후,
$$ \cos\theta=\frac{d_1\cdot d_2}{\|d_1\|\|d_2\|}=\frac{v_1^T\omega v_2}{\sqrt{v_1^T\omega v_1}\sqrt{v_2^T\omega v_2}},\quad \text{where}\,\,\,\omega=(KK^T)^{-1} $$
이 식으로부터 $\theta$가 90도이므로 $v_1^T\omega v_2=0$ 임을 유도해낼 수 있다.
하지만 $\omega=(KK^T)^{-1}$ 였으므로, camera matrix $K$에 의해 만들어지는 matrix이고,
우리는 아직 $K$에 대한 정보가 없다.
과연 두 vanishing points를 아는 것이 정확한 camera parameters추정하기에 충분할까?
앞서 우리는 $K$가 5의 자유도를 갖는다고 했었다.
하지만 $v_1^T\omega v_2=0$ 는 하나의 constraint밖에 주지 못하므로 $K$를 추정하기에는 턱없이 부족하다.
그렇다면, 주어진 두 평면과 수직한 또 다른 평면의 vanishing point $v_3$를 찾을 수 있다면 어떨까?
세 평면이 서로 수직하므로 $v_1^T\omega v_2=v_1^T\omega v_3=v_2^T\omega v_3=0$ 을 유도할 수 있다.
하지만 여전히 5개보다 모자란 3개의 constraint밖에 얻지 못했다.
이 때, 우리가 camera가 zero-skew이고 square pixel을 가졌다고 가정한다면 어떨까?
위 가정은 2개의 추가적인 constraint를 주기 때문에 이제 camera parameters를 추정할 수 있다.
위의 가정에 따라, $\omega$는 원래 아래와 같은 형태에서
$$ \omega=\begin{bmatrix}\omega_1&\omega_2&\omega_4\\\omega_2&\omega_3&\omega_5\\\omega_4&\omega_5&\omega_6\end{bmatrix} $$
(한 matrix의 전치행렬과의 곱이므로 symmetric한 꼴을 띄게 됨)
다음과 같은 형태를 가지게 된다.
$$ \omega=\begin{bmatrix}\omega_1&0&\omega_4\\0&\omega_1&\omega_5\\\omega_4&\omega_5&\omega_6\end{bmatrix} $$
(zero-skew와 square pixel은 $\omega_2=0$ 과 $\omega_1=\omega_3$ 이라는 정보를 줌)
따라서 위의 $\omega$에서는 4개의 변수만이 남아있게 된다.
$v_1^T\omega v_2=v_1^T\omega v_3=v_2^T\omega v_3=0$ 를 통해 $\omega$를 추론하면 $\omega$의 up to scale밖에 구하지 못하나,
어차피 결국 $K$는 homogeneous coordinate에 해당하는 것이므로 마지막 좌표로 나눠주기만 하면 되는 것이기 때문에 상관이 없다.
따라서 $\omega$를 구했으므로, Cholesky decomposition을 통해 $K$를 구해낼 수 있고,
결과적으로 single image를 통해 camera를 calibrate할 수 있다.
위와 같은 과정에 의해 $K$가 구해지면, 이런 scene으로부터 3D geometry를 reconstruct할 수 있게 된다.
(예를 들어, 위에서 언급한 평면들의 방향을 계산해낼 수 있음)
따라서, 이 single image로부터 알 수 있는 사실(평행한 직선 등)을 이용해 손쉽게 풍부한 정보를 얻어낼 수 있다.
'3D\Multiview Geometry > CS231A' 카테고리의 다른 글
| CH03. Epipolar Geometry (2) (0) | 2023.02.24 |
|---|---|
| CH03. Epipolar Geometry (1) (0) | 2023.02.12 |
| CH02. Single View Metrology (1) (0) | 2023.02.08 |
| CH01. Camera Models (4) (0) | 2023.02.06 |
| CH01. Camera Models (3) (0) | 2023.02.06 |
