Introduction
앞선 강까지는 single view metrology나 typical camera calibration을 통해 image로부터 3D world의 property를 유도해내는 과정을 보였었다.
하지만, 일반적으로 하나의 이미지를 이용해서는 3D world의 전체적인 구조를 복구해내기 어렵다.
바로 3D에서 2D로의 mapping의 intrinsic ambiguity 때문이다. (정보가 손실됨)

위의 그림을 보면, 남자가 피사의 사탑을 받치고 있는 것처럼 보인다.
하지만 실제로 남자가 피사의 사탑을 받치고 있는 것이 아니라,
다른 depth를 image plane에 투사시켰기 때문에 생기는 현상이다.
만약 이 scene을 다른 각도에서 볼 수 있다면, 이렇게 착시현상이 아니라 제대로 된 scene을 확인할 수 있을 것이다.
이번 강에서는 여러 개의 카메라가 있을 때 얼마나 기하학적 정보를 많이 주며, 이게 얼마나 유용한지에 대해 알아볼 것이다.
Epipolar Geometry

종종 multiple view geometry에서, 여러 대의 카메라와, 3D point, 그리고 각 카메라의 image plane으로의 해당 point의 projection간에는 흥미로운 관계가 성립된다.
Stereopair(쌍안 사진)에서 이와 같은 관계를 다루는 기하학을 epipolar geometry(등극선 기하)라고 한다.
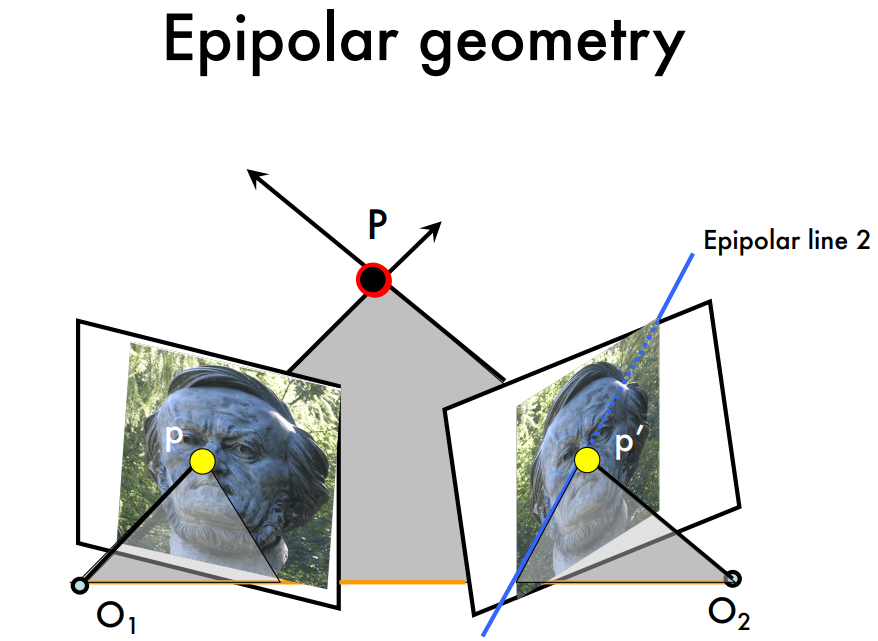
기본적으로 epipolar geometry에는 같은 한 3D point $P$를 바라보는 두 개의 카메라와,
각각의 image plane으로의 projection인 $p,p^\prime$ 가 있다.
먼저 용어 정리를 해보자.
- 각 카메라의 중심을 $O_1,O_2$
- $O_1,O_2$를 잇는 직선을 baseline
- $O_1,O_2,P$ 로 형성되는 평면을 epipolar plane
- Baseline과 각 image plane의 교점을 각각 epipole $e,e^\prime$
- Epipolar plane과 두 image plane과의 intersect를 epipolar lines(파란선)
그리고 epipolar lines는 baseline과 각각의 epipole에서 만난다는 성질도 가진다.
만약, 두 개의 image plane이 평행하다면 어떨까?

만약 두 image plane이 평행하다면, 그림과 같이 두 epipoles $e,e^\prime$은 무한대에 위치하게 된다.
(baseline이 두 image plane과 평행하기 때문에 무한대에서 만남)
또 하나의 특징은, epipolar lines가 각 image plane의 $u$축과 평행하다는 것이다.
(이렇게 평행한 경우가 주는 정보가 많고 특별하기 때문에 추후에 다른 section에서 더 언급할 예정)

그러나 실제로 real world situation에서는 점 $P$의 정확한 3D 위치가 주어지지 않는다.
하지만 다행히도 하나의 image plane 위로 이 점을 project한 $p$를 결정할 순 있다.
또한 camera들의 위치, 방향, 그리고 camera matrix 도 알고 있어야한다.
먼저, camera들의 위치와 image point $p$를 통해 epipolar plane을 형성할 수 있다.
이 epipolar plane으로 epipolar lines 또한 찾아낼 수 있다.
정의에 따라, $P$를 두 번째 image plane으로의 project 한 $p^\prime$은 두 번째 이미지의 epipolar line 위에 있어야한다.
따라서, scene에 대한 3D structure 정보 없이 epipolar geometry에 대한 기본적인 이해만으로도 두 이미지 간의 강력한 constraint을 만들어낼 수 있는 것이다.


그럼 한번 points와 epipolar lines를 mapping하는 법에 대해 알아보자.
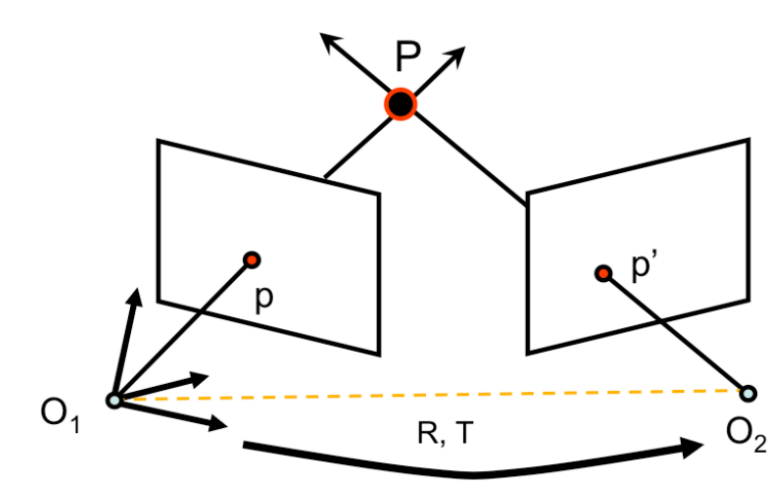
먼저, 각각의 카메라의 3D에서 2D image plane으로의 projection matrix를 $M,M^\prime$이라고 하자.
$P_w$는 world frame의 점, $P_c$는 first camera frame에서의 점, $P_{c^\prime}$은 second camera frame에서의 점이라고 하고,
$w,c,c^\prime$을 각각 world, first, second camera reference frame이라고 하자.
World reference system과 first camera reference system이 같다고 가정해보자.($w,c$가 같음)
그리고 두 번째 카메라는 world frame으로 부터 회전 $R_{wc^\prime}$을 하고, 이동 $T_{wc^\prime}$을 한 만큼 떨어져 있다.
그렇다면, world frame에서서 특정된 점을 second camera reference frame으로 transform한 결과를
$$ P_{c^\prime}=R_{wc^\prime}^{-1}(P_w-T_{wc^\prime})=R_{wc^\prime}^{T}P_w-R_{wc^\prime}^{T}T_{wc^\prime} $$
로 정의할 수 있다. (point를 변환한 거는 역변환이라는데… 잘 이해가 안된다.)
반대로, second camera frame에서 world frame coordinate으로 바꾸면
$$ P_w=R_{wc^\prime}P_{c^\prime}+T_{wc^\prime} $$
과 같다.
따라서, camera projection matrix를 다음과 같이 표현할 수 있다.
$$ M=K\begin{bmatrix}I&0\end{bmatrix}\quad\quad M^\prime=K^\prime\begin{bmatrix}R_{wc^\prime}^{T}&-R_{wc^\prime}^{T}T_{wc^\prime}\end{bmatrix} $$
The Essential Matrix
가장 simple한 경우를 생각해보자.
즉, 우리가 canonical camera를 갖고 있다고 가정해보자. ($K=K^\prime=I)$
그러면 camera matrix가 다음과 같이 간소화된다.
$$ M=\begin{bmatrix}I&0\end{bmatrix}\quad\quad M^\prime=\begin{bmatrix}R_{wc^\prime}^{T}&-R_{wc^\prime}^{T}T_{wc^\prime}\end{bmatrix} $$
두 번째 카메라의 프레임에서 정의된 $p^\prime$이 world frame에서는 $p=R_{wc^\prime}p^\prime+T_{wc^\prime}$ 이 된다.
그리고 $T_{wc^\prime}$도 world frame에서 첫 번째 optical center로부터 두 번째 optical center로의 vector이다.
즉 이 두 벡터가 모두 epipolar plane위에 있기 때문에, cross product를 해주면,
$T_{wc^\prime}\times(R_{wc^\prime}p^\prime+T_{wc^\prime})=T_{wc^\prime}\times R_{wc^\prime}p^\prime$ 이 되고, 이는 epipolar plane의 normal vector이다.
즉 $p$는 $T_{wc^\prime}\times R_{wc^\prime}p^\prime$에 normal하고, 다음과 같은 constraint를 유도할 수 있다.
$$ p^T(T_{wc^\prime}\times R_{wc^\prime})p^\prime=0 $$
Cross product를 matrix-vector multiplication으로 표현하면 다음과 같이 나타난다.
$$ \text{a}\times\text{b}=\begin{bmatrix}0&-a_x&a_y\\a_z&0&-a_x\\-a_y&a_x&0\end{bmatrix}\begin{bmatrix}b_x\\b_y\\b_z\end{bmatrix}=[\text{a}_{\times}]\text{b} $$
이걸 활용해서 위의 constraint을 다시 표현해보면,
$$ p^T([T_{\times}] R_{wc^\prime})p^\prime=0 $$
이고, 이때 $E=[T_{\times}] R_{wc^\prime}$ 를 Essential Matrix라고 부른다.
다시 정리해보면, epipolar constraint은
$$ p^TEp^\prime=0 $$
이다.
Essential matrix는 $3\times 3$ 행렬이고, 5의 자유도를 가지며, singular 하고 rank가 2이다.
이 essential matrix는 $p,p^\prime$과 연관된 epipolar line을 계산하는데 매우 유용하다.
예를 들어, $\ell^\prime=E^Tp$ 는 두 번째 카메라의 image plane의 epipolar line이다.
비슷하게, $\ell=Ep^\prime$은 첫 번째 카메라의 image plane의 epipolar line이다.
Essential matrix의 또다른 property는, epipole과의 내적이 0이라는 것이다.($Ee^\prime=E^Te=0$)
왜냐하면 모든 camera 1의 image의 $x$에서, camera 2에서 상응하는 epipolar line에 대해, $\ell^\prime=E^Tx$는 반드시 epipole $e^\prime$을 포함하기 때문이다.
따라서, 모든 $x$에 대해 $e^\prime$은 $(E^Tx)^Te^\prime=x^T(Ee^\prime)=0$ 을 만족하고 $Ee^\prime=0$을 만족한다.
비슷하게, $E^Te=0$ 또한 만족한다.
'3D\Multiview Geometry > CS231A' 카테고리의 다른 글
| CH04. Stereo Systems (1) (1) | 2023.03.02 |
|---|---|
| CH03. Epipolar Geometry (2) (0) | 2023.02.24 |
| CH02. Single View Metrology (2) (0) | 2023.02.09 |
| CH02. Single View Metrology (1) (0) | 2023.02.08 |
| CH01. Camera Models (4) (0) | 2023.02.06 |
