CH04. Stereo Systems (1)

지난 번까지는 여러 추가적인 viewpoints 들이 얼마나 해당 scene에 대한 정보를 많이 줄 수 있는지에 대해서 알아봤었다.

Epipolar geometry는 3D scene에 대한 정보 없이 한 image plane의 점들을 다른 image plane으로 대응했었다면, 이번 강에서는 여러 2D images를 이용해서 3D scene을 recover 하는 법에 대해 알아본다.  

 

Triangulation

Triangulation은 multiview geometry에서 가장 fundamental한 문제 중 하나다.

Triangulation은 3D point가 projection된 두 개 이상의 images를 이용해서 해당 3D point의 위치를 결정하는 작업이다.

만약 두 개의 view를 이용한 triangulation의 경우, 두 개의 camera가 있을 것이고 각각은 camera intrinsic parameter인 $K,K^{\prime }$ 를 갖는다.

그리고 서로에 대한 $R,T$ 도 정의할 수 있다.

3D 상의 점 $P$의 camera image plane으로의 projection이 각각 $p,p^{\prime }$ 라고 하자.

$P$의 정확한 위치를 알 수는 없지만, $p,p^{\prime }$의 정확한 위치는 알 수 있다.

그리고 $K,K^{\prime },R,T$도 알고 있으므로 각 카메라의 center $O_1,O_2$와 $p,p^{\prime }$을 잇는 직선인 $\ell ,{\ell }^{\prime }$을 계산해낼 수 있다.

따라서 $P$는 $\ell$과 ${\ell }^{\prime }$의 교점이므로 $P$를 구해낼 수 있다.

하지만 이 방법이 수학적으로도 당연하고, 직관적이긴 하나 실제로는 잘 안 된다.

왜냐하면 real world에서는 $p$와 $p^{\prime }$를 얻을 때 noise가 생기기 마련이고, camera parameters들이 정확하지 않기 때문에 $\ell$과 ${\ell }^{\prime }$의 교점을 찾는 게 쉽지 않다.

대부분의 경우, 두 직선이 교차하지 않을 확률이 더 크므로 $P$를 찾지 못한다.

그렇다면 이를 어떻게 해결할 수 있을지를 고민해보자.  

 

A linear method for triangulation

간단한 linear triangulation method를 알아보자.

두 점 $p=MP=(x,y,1)$과 $p^{\prime }=M^{\prime }P=(x^{\prime },y^{\prime },1)$은 주어진다.

Cross product의 정의에 따르면 $p\times (MP)=0$ 가 된다.

따라서

$$\begin{gathered} x(M_{3}P)-(M_{1}P)=0 \\ y(M_{3}P)-(M_{2}P)=0 \\ x(M_{2}P)-y(M_{1}P)=0 \end{gathered}$$

과 같은 constraint를 얻을 수 있다.($M_i$는 행렬 $M$의 $i$번째 row)

$p^{\prime }$과 $M^{\prime }$으로도 비슷한 constraint를 만들어 낼 수 있다.

이 constraint들을 이용하면 $AP=0$ 꼴의 linear equation을 세울 수 있다.

$$A=\left[\begin{array}{c}x{M}_3-M_1\\ y{M}_3-M_2\\ x^{\prime }{M}_3^{\prime }-M_1^{\prime }\\ y^{\prime }{M}_3^{\prime }-M_2^{\prime }\end{array}\right]$$

이거는 이제 SVD 이용하면 된다.

이 방법이 좋은 또 다른 이유는 여러 view를 통해 얻은 여러 projection들도 그냥 행렬을 아래로 쌓기만 하면 되므로 처리하기가 쉽다.  

 

하지만, 이 방법은 projective-invariant하지 않기 때문에 projective reconstruction에는 적합하지 않다.

예를 들어, 카메라 행렬 $M,M^{\prime }$을 projective transformation 된 행렬 $M{H}^{-1},M^{\prime }{H}^{-1}$로 바꿔보자.

그러면 $A$는 $A{H}^{-1}$이 될 것이다.

따라서 $AP=0$ 이었던 문제가 $(A{H}^{-1})(HP)=0$ 이 된다.

SVD는 $\Vert P\Vert =1$ 이라는 constraint이 있는데, 이는 projective matrix $H$ 하에서는 만족하지 않는다.(not invariant)

따라서 이 방법은 간단하긴 하지만 대부분 optimal solution을 찾지는 못한다.  

 

A nonlinear method for triangulation

대신 real-world에서 triangulation은 대부분 다음과 같은 minimization problem으로 표현된다.

$$\underset{\hat{P}}{\text{min}}\Vert M\hat{P}-p{\Vert }^2+\Vert M^{\prime }\hat{P}-p^{\prime }{\Vert }^2$$

위 식은 각 $\hat{P}$을 image로 reproject한 reprojection error를 통해 $P$를 가장 근사하는 3D 상의 점 $\hat{P}$를 찾는 것이다.

3D point의 reprojection error는 해당 점의 projection과 대응하는 점의 image plane에서의 관찰되는 point와의 distance를 의미한다.

위의 Figure2에서를 예로 들면, $M\hat{P}$가 $\hat{P}$의 projected point가 되고, $\hat{P}$과 대응되는 관찰되는 점은 $p$가 된다.

따라서 image1에서의 reprojection error은 $\Vert M\hat{P}-p\Vert$ 가 되는 것이다.

(위의 식은 모든 image의 reprojection error을 합한 것을 의미)

그렇기 때문에 더 일반화해서 식을 표현해보면

$$\underset{\hat{P}}{\text{min}}\sum _i\Vert M{\hat{P}}_i-p_i{\Vert }^2$$

처럼 쓸 수 있다.  

 

실제로는, 굉장히 좋은 근사치를 내는 정교한 optimization technique들이 존재하지만 이 강의에서는 이 중 하나의 기법에만 집중하기로 한다.

우리가 사용할 최적화 기법은 Gauss-Newton 알고리즘이다.

일반적인 nonlinear least squares problem의 경우는

$$\Vert r(x){\Vert }^2=\sum _{i=1}^m{r}_i(x{)}^2$$

를 minimize하는 $x\in {\mathbb{R}}^n$ 을 찾는 것이다.

($r$은 $r(x)=f(x)-y$ 를 만족하는 $r:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 의 residual function이다.

이 때, $f$는 function, $x$는 input, $y$는 observation)

함수 $f$가 linear하다면, nonlinear least squares problem은 일반적인 linear least squares problem로 간소화된다.

하지만, image plane으로의 projection은 homogeneous coordinate으로 나눠줘야 하므로 대부분의 projection은 nonlinear하다.

따라서 카메라 행렬은 affine하지 않다.  

 

$e_i=M{\hat{P}}_i-p_i$ 의 $2\times 1$ 벡터 $e_i$를 정의하면, 최적화문제를 다음과 같이 변경할 수 있다.

$$\underset{\hat{P}}{\text{min}}\sum _i{e}_i(\hat{P}{)}^2$$

그리고 이 식은 완벽한 nonlinear least squares problem 꼴이 된다.  

 

그러면 어떻게 Gauss-Newton algorithm을 적용하는지 알아보자.

먼저, 앞에서 봤던 간단한 linear method로 대충 어림잡아 구한 꽤나 합리적인 $\hat{P}$가 있다고 하자.

Gauss-Newton algorithm은 estimate를 더 나은 방향(reprojection error을 minimize하는)으로 update 해나가는 것이다.

각 step마다 우리는 $\hat{P}$를 ${\delta }_P$ 만큼 업데이트 하려고 한다. ($\hat{P}=\hat{P}+{\delta }_P$)

그렇다면 update parameter ${\delta }_P$는 어떻게 설정하는 걸까?

Gauss-Newton 알고리즘의 key insight는 현재의 추정치인 $\hat{P}$ 근처의 residual function을 linearize하는 것이다.

우리의 optimization problem의 경우에는,

$$e(\hat{P}+{\delta }_P)\approx e(\hat{P})+{\displaystyle \frac{\partial e}{\partial P}}{\delta }_P$$

처럼 point $P$의 residual error $e$를 근사할 수 있고, minimization problem이

$$\underset{{\delta }_P}{\text{min}}\Vert {\displaystyle \frac{\partial e}{\partial P}}{\delta }_P-(-e(\hat{P})){\Vert }^2$$

와 같이 변환된다.

이렇게 residual을 정의하면, 일반적인 linear least squares problem의 꼴과 같다.

따라서 $N$개의 이미지에 대한 triangulation problem에서 linear least squares solution은

$${\delta }_P=-(J^{T}J{)}^{-1}{J}^{T}e$$

이고 이 때 $e$와 $J$는

$$e=\left[\begin{array}{c}{e}_1\\ ⋮\\ e_N\end{array}\right]=\left[\begin{array}{c}{p}_1-M_1\hat{P}\\ ⋮\\ p_n-M_n\hat{P}\end{array}\right],J=\left[\begin{array}{ccc}{\displaystyle \frac{\partial e_1}{\partial {\hat{P}}_1}}& {\displaystyle \frac{\partial e_1}{\partial {\hat{P}}_2}}& {\displaystyle \frac{\partial e_1}{\partial {\hat{P}}_3}}\\ ⋮& ⋮& ⋮\\ {\displaystyle \frac{\partial e_N}{\partial {\hat{P}}_1}}& {\displaystyle \frac{\partial e_N}{\partial {\hat{P}}_2}}& {\displaystyle \frac{\partial e_N}{\partial {\hat{P}}_3}}\end{array}\right]$$

이다.

특정 이미지의 residual error vector $e_i$는 $2\times 1$ vector임을 유의하자. (image plane의 차원은 2D이므로)

결과적으로 two camera의 triangulation의 경우에는 ($N=2)$ residual vector $e$가 $2N\times 1=4\times 1$ vector이고, Jacobian $J$는 $2N\times 3=4\times 3$ 행렬이 된다.

이 경우도 새로운 image에 대해서 $e,J$에 행만 추가해주면 되기 때문에 매우 유용하다.

이렇게 update ${\delta }_P$를 계산하고 나면, 정해진 step만큼 혹은 충분히 수렴할 때까지 이 과정을 반복해주면 된다.

Gauss-Newton 알고리즘의 중요한 특성은, 우리의 estimate 근처에서 residual function이 linear 하다고 했던 가정은 수렴을 보장하지 않는다는 것이다.

따라서 정해진 update의 횟수를 정해놓고 하는 것이 실제로는 더 유용하다.  

 

Affine structure from motion

앞 section에서는 3D scene의 정보를 얻기 위해 두 개 이상의 view를 어떻게 활용할 수 있는지 보았다. 이제는 이를 더 확장해보자.

Multiple view로부터 획득한 observations of points를 결합함으로써, **Structure from motion(SFM)**이라는 방법을 통해 해당 scene의 3D structure 뿐만 아니라 카메라의 parameter까지도 결정할 수 있다.

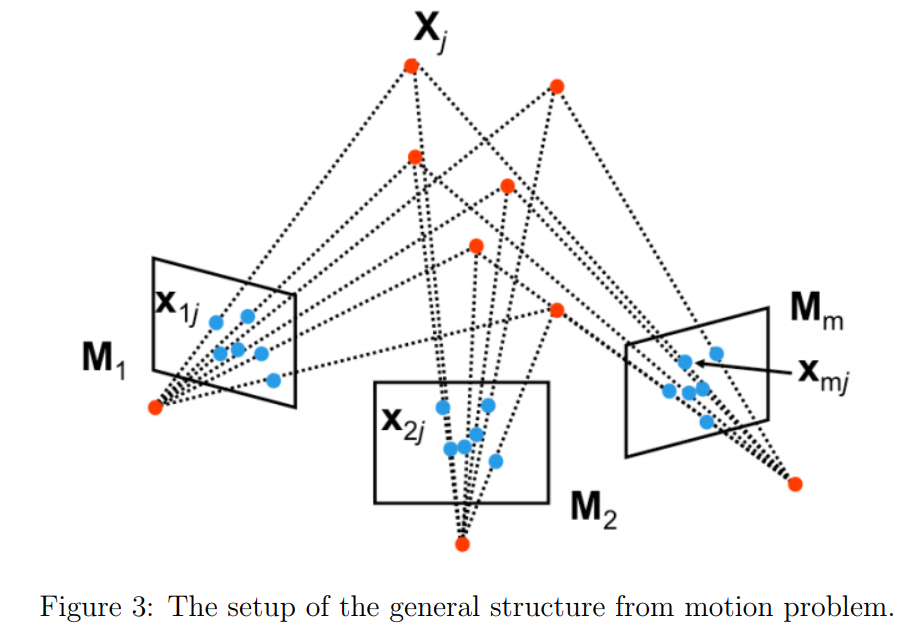
우리가 $m$개의 카메라가 있고 각 카메라의 intrinsic, extrinsic 특성을 포함한 camera transformation $M_i$까지 알고 있다고 해보자.

$X_j$를 scene의 $n$개의 3D 점 중 하나라고 하자.

각 3D 점은 각 카메라에 location $x_{ij}$로 보일 것이다. (projective transformation $M_i$를 통한 camera $i$ image로의 $X_j$ projection)

SFM의 목적은 모든 observations $x_{ij}$를 이용해 scene을 recover하는 것($n$개의 3D 점 $X_j$)과 camera의 motion을 recover하는 것($m$개의 projection matrix $M_i$)이다.  

 

The affine structure from motion problem

General한 SFM을 다루기 전에 좀 쉬운 문제를 먼저 살펴보자.

여기서는 카메라가 affine하거나 weak-perspective임을 가정한다.

Full perspective model의 경우는

$$M=\left[\begin{array}{cc}A& b\\ v& 1\end{array}\right]$$

이었다. ($v$는 non-zero $1\times 3$ vector)

반면 weak perspective model의 경우 $v=0$ 이다.

따라서 이 성질을 이용해서 $MX$의 homogeneous coordinate을 계산해보면

$$x=MX=\left[\begin{array}{c}{m}_1\\ m_2\\ 0001\end{array}\right]\left[\begin{array}{c}{X}_1\\ X_2\\ X_3\\ 1\end{array}\right]=\left[\begin{array}{c}{m}_1{X}_1\\ m_2{X}_2\\ 1\end{array}\right]$$

과 같다. 또는 이를

$$M_{}=\left[\begin{array}{cc}A& b\end{array}\right]X=AX+b$$

와 같이 나타낼 수도 있다. (camera matrix를 $M_{\text{affine}}=\left[\begin{array}{cc}A& b\end{array}\right]$로 표현)  

 

SFM으로 돌아와서, 우리는 $m$개의 $M_i$ 행렬과 $n$개의 world좌표 $X_j$ 을 추정해야하고, 이는 즉 $mn$개의 observation으로부터 $8m+3n$개의 미지수를 찾아야 함을 의미한다.

앞서 각 observation으로부터 2개의 constraint를 얻을 수 있음을 확인했었다.

따라서 총 $2mn$개의 equation을 얻을 수 있다.

이 식으로부터 최소 몇 개의 observation이 필요한지를 계산할 수 있는데, 예를 들어 $m=2$ 개의 카메라가 있다면 최소 $n=16$ 개의 3D 점이 필요하다는 것을 의미한다.

그럼 이렇게 충분한 대응점이 있을 때, 문제를 푸는 방법에 대해 알아보자.  

 

The Tomasi and Kanade factorization method

여기서는 Tomasi와 Kanade의 factorization method에 대해 알아본다.

이 method는 크게 두 단계로 구성된다.

1. data centering step
2. actual factorization step

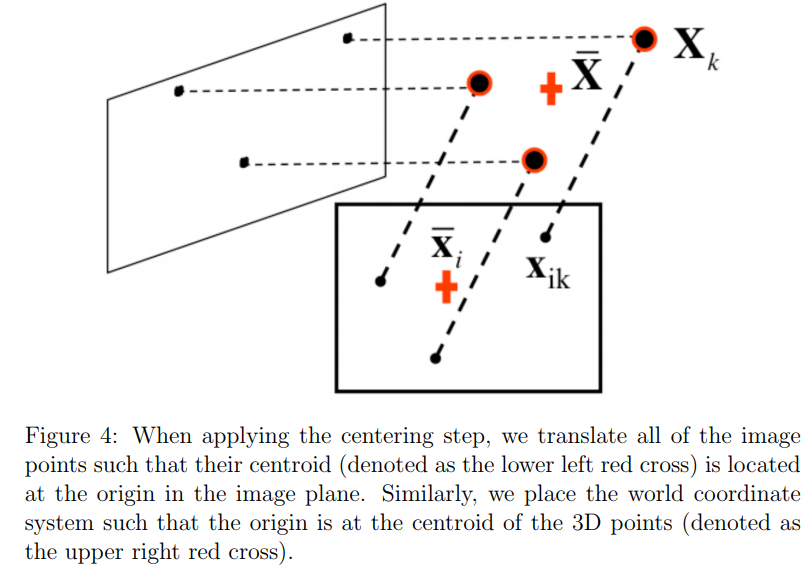
먼저 data centering step에 대해서 알아보자.

이 단계에서 main idea는 원점으로 데이터를 center시키는 것이다.

그러기 위해서 각 이미지 $i$에서 새로운 좌표 ${\hat{x}}_{ij}$를 다음과 같이 정의한다.

$$\hat{x}ij=xij-\bar{x}i=xij-{\displaystyle \frac{1}{n}}\sum _{j=1}^n{x}_{ij}$$

Affine SFM 의 경우 카메라 행렬의 $A_i,b_i$ 를 통해

$$x_{ij}=A_i{X}_j+b_i$$

과 같이 표현할 수 있다.

따라서

$$\begin{array}{rl}\hat{x}ij& =xij-{\displaystyle \frac{1}{n}}\sum _{k=1}^n{x}_{ik}\\ & =A_i{X}_j-{\displaystyle \frac{1}{n}}\sum _{k=1}^n{A}_i{X}_k\\ & =A_i(X_j-{\displaystyle \frac{1}{n}}\sum _{k=1}^n{X}_k)\\ & =A_i(X_j-\bar{X})\\ & =A_i{\hat{X}}_j\end{array}$$

과 같이 유도할 수 있다.

이처럼 월드 좌표계의 원점을 centroid $\bar{X}$로 옮기면, $\hat{x}ij$와 $\hat{X}ij$가 $2\times 3$ 행렬 $A_i$만으로 연관이 된다.

궁극적으로, 이 centering step은 compact한 행렬곱으로 표현하게 해준다.

하지만, ${\hat{x}}_{ij}=A_i{\hat{X}}_j$ 에서 우리는 오로지 좌변의 값만 알 수 있다.

따라서 우리는 어떻게든 $A_i$와 ${\hat{X}}_{ij}$로 분리를 해야 한다.

모든 카메라의 모든 observation을 이용해 measurement matrix $D$를 세워보면

$$D=\left[\begin{array}{cccc}\hat{x}11& \hat{x}12& \cdots & \hat{x}1n\\ \hat{x}21& \hat{x}22& \cdots & \hat{x}2n\\ & & \ddots & \\ \hat{x}m1& \hat{x}m2& \cdots & {\hat{x}}_{mn}\end{array}\right]$$

이 된다.

Affine assumption에 따라 $D$는 $2m\times 3$의 motion matrix $M$ ($A_1,\cdots ,A_m$으로 구성)과 $3\times n$의 structure matrix $S$ ($X_1,\cdots ,X_n$으로 구성)로 표현 가능하다.

중요한 점은 $D$의 rank가 3이라는 것인데, $D$가 차원이 3인 두 행렬의 곱이기 때문이다.  

 

$D$를 $M$과 $S$로 factorize하기 위해 SVD를 쓸 것이다. ($D=U\mathrm{\Sigma }{V}^T$)

Rank가 3인 것을 알고 있으므로, 단 3개의 non-zero singular value가 $\mathrm{\Sigma }$에 있을 것이다.

따라서 다음과 같이 분해를 할 수 있다.

$$\begin{array}{rl}D& =U\mathrm{\Sigma }{V}^T\\ & =\left[\begin{array}{ccc}{u}_1& \cdots & u_n\end{array}\right]\left[\begin{array}{cccccc}{\sigma }_1& 0& 0& 0& \cdots & 0\\ 0& {\sigma }_2& 0& 0& \cdots & 0\\ 0& 0& {\sigma }_3& 0& \cdots & 0\\ 0& 0& 0& 0& \cdots & 0\\ & & & & \ddots & \\ 0& 0& 0& 0& \cdots & 0\end{array}\right]\left[\begin{array}{c}{v}_1^T\\ ⋮\\ v_n^T\end{array}\right]\\ & =\left[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}\right]\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right]\left[\begin{array}{c}{v}_1^T\\ v_2^T\\ v_3^T\end{array}\right]\\ & =U_3{\mathrm{\Sigma }}_3{V}_3^T\end{array}$$

하지만 실제로는 noise와 affine camera approximation에 의해 D의 rank가 3보다 크다.

하지만, rank가 3보다 클 때도, $U_3{W}_3{V}_3^T$가 Frobenius norm 측면에서 여전히 제일 좋은 rank-3 approximation이다.

${\mathrm{\Sigma }}_3{V}_3^T$가 $3\times n$ 행렬이고 $U_3$가 $2m\times 3$ 행렬이다.

이렇게 크기를 따져서 $M,S$로 분해하는 것이 affine SFM에서는 타당하게 들릴 수 있지만, UNIQUE한 solution은 주지 않는다.

왜냐하면 $M=U_3{\mathrm{\Sigma }}_3$ 그리고 $S=V_3^T$로 잡을 수도 있기 때문이다.

그렇다면 뭘 골라야 할까?

Tomasi와 Kanade의 논문에서 그들은 robust한 선택은 $M=U_3\sqrt{{\mathrm{\Sigma }}_3}$와 $S=\sqrt{{\mathrm{\Sigma }}_3}{V}_3^T$로 잡는 것이라고 한다.  

 

Ambiguity in reconstruction

그럼에도 불구하고, $D=MS$ factorization은 여전히 ambiguity가 존재한다.

$$D=MA{A}^{-1}S=(MA)(A^{-1}S)$$

와 같이 invertible한 임의의 행렬 $A$를 사이에 집어넣을 수 있기 때문이다.

따라서 우리의 solution은 underdetermined하므로 추가적인 constraints가 필요하다.

이렇게 reconstruction이 affine ambiguity가 있다는 말은, 즉 평행성은 보존이 되고 metric scale은 알 수가 없다는 것을 의미한다.

Reconstruction에서 또 다른 중요한 ambiguity중 하나는 similarity ambiguity이다.

(rotation, translation, scaling와 같은 similarity transform에 따라 생김)

이 ambiguity는 카메라가 intrinsically calibrated 되어 있어도 존재한다.

(다행인 것은 카메라가 calibrated되어 있는 경우라면 이 ambiguity가 유일한 ambiguity임)

만약 추가적인 가정(figure에 있는 집의 높이를 안다던가)이나 추가적인 데이터를 병합하지 않는 이상 object의 scale, 정확한 위치, 표준 방향 등을 정확히 알 수는 없다.

물체를 앞뒤로 옮기는 대신 scale을 조정해주는 식으로 같은 이미지를 얻을 수 있기 때문이다.

이런 예가 바로 camera calibration이다.

Calibration을 할 때, 체커보드의 정확한 월드 좌표계에서의 위치를 알 수 있으므로 사각형의 크기에 대한 정보를 우리가 알고 있다.

따라서 우리가 metric scale을 알 수 있는 것이다.

  

  

 

Tomasi and Kanade factorization method 구현 코드가 궁금하다면,

https://github.com/ianpark318/CS231A/blob/main/ps2/ps2_code/PSET2.ipynb 참고