고윳값과 고유벡터

고윳값과 벡터

정의

체 $F$에 대한 벡터공간 $V$위의 선형사상 $L:V\to V$에 대해 다음 두 조건

1. $v\ne \overrightarrow{0}$
2. $L(v)=\lambda v$

를 만족하는 $\lambda \in F$와 $v\in V$ 를 각각 고윳값과 고유벡터라고 한다.

(그래도 영어가 편하니까 고윳값은 eigenvalue, 고유벡터는 eigenvector로 표현)  

 

행렬로 생각해보면,

 

고유방정식

영어로 characteristic equation이라고 부른다.

$n\times n$ 행렬 $A$에 대해 $\lambda$가 $A$의 eigenvalue이기 위한 필요충분조건은 다음 방정식

$$det(A-\lambda I)=0$$

을 만족하는 것이다.

(why? $Av=\lambda v$ 는 $(A-\lambda I)v=0$ 이고, 정의에 따라 $v$는 영벡터가 아니므로 $det(A-\lambda I)=0$ 만족해야 함)

이 방정식을 고유방정식이라고 하며, 좌변의 식을 고유다항식이라고 한다.

(eigenvalue는 특수한 값이지만 유일한 값은 아님)  

 

고유공간

선형사상 $L-\lambda I$ 의 핵(kernel)을 eigenvalue $\lambda$의 고유공간이라고 한다.

따라서, 고유공간($L-\lambda I$의 null space)의 영벡터가 아닌 벡터는 eigenvector이다.

또한, $L$의 eigenvector들로 구성된 $V$의 basis를 선형사상 $L$의 고유기저(eigenbasis)라고 한다.

 

알고리즘

Eigenvalue와 Eigenvector를 찾는 알고리즘은 다음과 같다.

 

예제) $A=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$

  

예제) $A=\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$

  

예제) $A=\left[\begin{array}{ccc}1& 0& 3\\ 1& -1& 2\\ -1& 1& -2\end{array}\right]$

 

  

Complex Eigenvalues

벡터와 행렬의 원소로 복소수도 가능하도록, field of scalar를 복소수까지 확장해서 생각해보자.

그러면 $n\times n$ 실수 행렬 $A$는 $n$개의 eigenvalue를 가질 것이고,

어떤 eigenvalue는 중복될 수도 있고, 복소수를 가질 수도 있다.

유의할 점은, 만약 $\lambda =a+bi(b\ne 0)$ 가 eigenvalue라면, 반드시 $\bar{\lambda }=a-bi(b\ne 0)$ 또한 $A$의 eigenvalue가 되어야 한다.

또, 만약 $\text{z}$가 $\lambda$에 해당하는 eigenvector일 때, $A\bar{\text{z}}=\bar{\lambda }\bar{\text{z}}$ 도 만족한다.  

  

 

예제) $A=\left[\begin{array}{cc}1& 2\\ -2& 1\end{array}\right]$

  

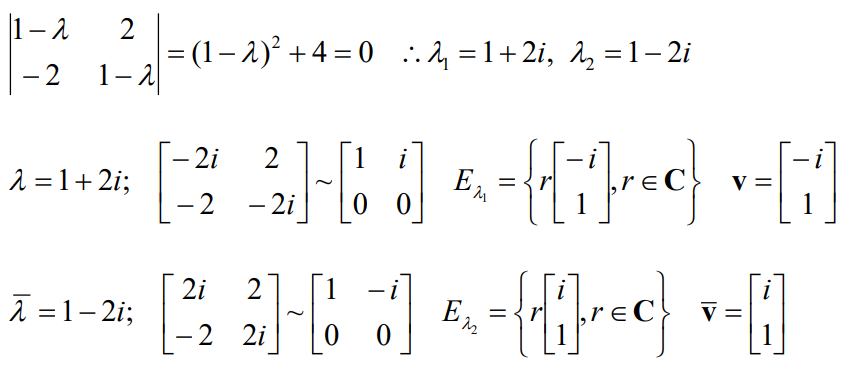
Product and Sum of Eigenvalues

$n\times n$ 행렬 $A$에 대해, $A$의 고유다항식(characteristic polynomial) $p(\lambda )$는 다음의 꼴을 가진다.

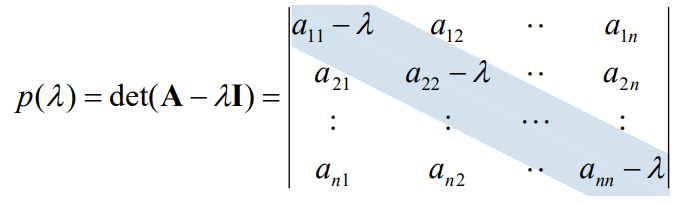
첫번째 열에 대해서, determinant 전개를 하면,

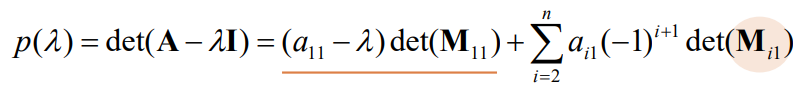
와 같다.

이 때, 소행렬 $\mathbf{M}i1$의 대각선 원소에서 $(a11-\lambda )$ 와 $(a_{ii}-\lambda )$는 나타나지 않는다.

$det({\mathbf{M}}_{11})$를 같은 방식으로 전개하면,

$$(a_{11}-\lambda )(a_{22}-\lambda )\cdots (a_{nn}-\lambda )$$

만이 $det(A-\lambda I)$의 전개식 가운데 대각원소 $(n-2)$ 개 이상의 곱으로 이루어진 항임을 알 수 있다.

따라서 $p(\lambda )$의 최고차항의 계수가 $(-1{)}^n$이다.

${\lambda }_1,{\lambda }_2,...,{\lambda }_n$이 $A$의 eigenvalue들이라면,

$$\begin{gathered} p(\lambda )=det(A-\lambda I)=(-1{)}^n(\lambda -{\lambda }_1)(\lambda -{\lambda }_2)\cdots (\lambda -{\lambda }_n) \\ =({\lambda }_1-\lambda )({\lambda }_2-\lambda )\cdots ({\lambda }_n-\lambda ) \end{gathered}$$

가 되므로, 따라서

$${\lambda }_1\cdot {\lambda }_2\cdots {\lambda }_n=p(0)=det(A-0I)=det(A)$$

가 성립한다.

즉, $A$의 행렬식은 $A$의 모든 eigenvalue의 곱과 같다.  

 

또 재밌는 사실은,

$(a_{11}-\lambda )(a_{22}-\lambda )\cdots (a_{nn}-\lambda )$에서 $(-\lambda {)}^{n-1}$의 계쑤는 $\sum a_{ii}$ 즉, 대각합 trace가 된다.

또, $p(\lambda )$로부터

$$\begin{gathered} p(\lambda )=(-1{)}^n(\lambda -{\lambda }_1)(\lambda -{\lambda }_2)\cdots (\lambda -{\lambda }_n) \\ =({\lambda }_1-\lambda )({\lambda }_2-\lambda )\cdots ({\lambda }_n-\lambda ) \end{gathered}$$

똑같이 $\sum {\lambda }_i$ 가 계수임을 알 수 있으므로,

$$\sum _{i=1}^n{\lambda }_i=\sum _{i=1}^n{a}_{ii}=\text{tr}(A)$$

라는 성질을 유도해낼 수 있다.

즉, $A$의 대각합은, 모든 eigenvalue의 합과 같다.  

   

 

예제) $A=\left[\begin{array}{cc}5& -18\\ 1& -1\end{array}\right]$

 

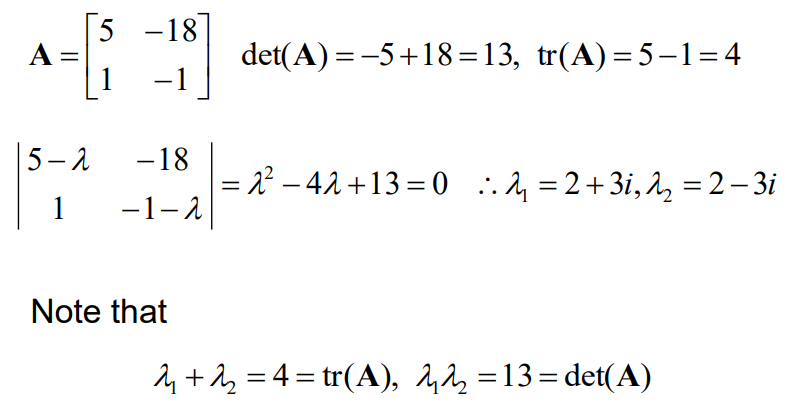
$A$의 행렬식이 모든 eigenvalue의 곱과 같다는 것으로부터 다음을 유도할 수 있다.

💡 정방행렬 $A$가 invertible하기 위한 필요충분조건은 $A$의 eigenvalue가 0이 아닌 것이다.

Eigenvalue에 0이 있으면, $det(A)=0$이 되기 때문이다.