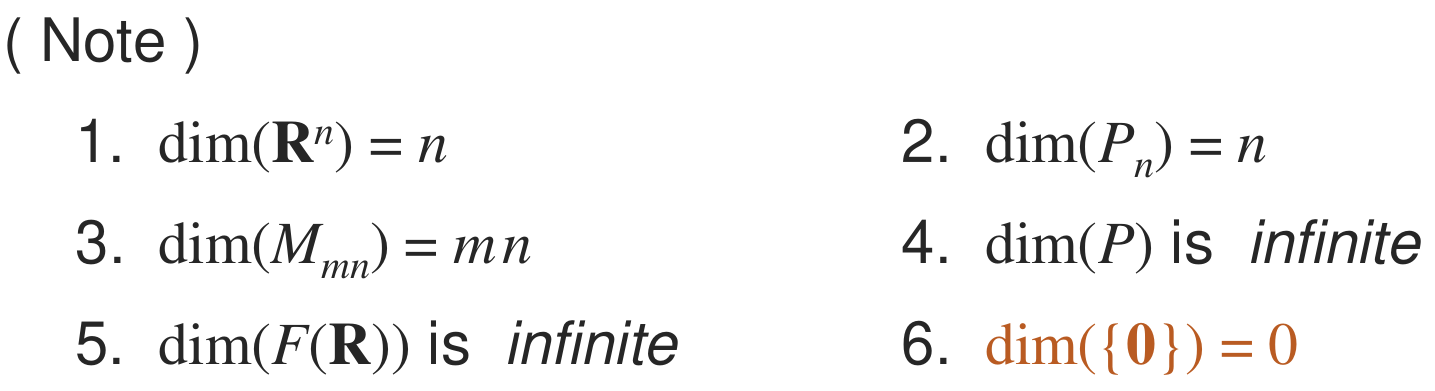벡터공간 (1)

Vector Space

$V$가 addition과 scalar multiplication이 정의된 집합이라고 할 때, 

 

1. Addition

두 개의 $V$에 속한 element $\text{u},\text{v}$의 합, 즉 $\text{u}+\text{v}$ 

 

2. Scalar multiplication

Scalar인 $c$와 $V$의 element $\text{u}$ 로 이루어진 rule로써, $c\text{u}$로 나타냄.

이와 같이, 두 operation이 정의되어 있고, 다음의 axiom들을 만족하면 Vector space라고 함.

 

---

Null space

• Matrix에서 정의된 subspace이다.
• $m\times n$ matrix $A$ 의 null space는 $A\text{x}=0$을 만족하는 모든 $\text{x}$ ($n-$벡터)로 구성되어 있다.

$$ \text{Null}(\text{A})=\{\text{x}\,|\,\text{A}\text{x}=0,\,\,\text{x}\in\mathbf{R}^n\} $$

• $\text{A}$의 null space는 $\mathbf{R}^n$의 subspace이다.  

 

---

Span and Spanning Set

$\text{v}_1,...,\text{v}_n$ 이 vector space $V$ 의 vector라고 하면, $a_1,...,a_n$이 scalar일 때,

$a_1\text{v}_1+...+a_n\text{v}_n$ 을 $\text{v}_1,...,\text{v}_n$ 의 linear combination이라고 한다.  

 

$\text{v}_1,...,\text{v}_n$ 의 모든 linear combination들을 $\text{v}_1,...,\text{v}_n$ 의 span 이라고 하고,

$\text{Span}(\text{v}_1,...,\text{v}_n)$ 이라고 표기한다.  

 

$W=\text{Span}(\text{v}_1,...,\text{v}_n)$ 일 때, $\text{v}_1,...,\text{v}_n$ 가 $W$ 를 span한다고 하고,

$\text{v}_1,...,\text{v}_n$를 $W$의 spanning set이라고 부른다.

 

  

💡
만약, $\text{v}_1,...,\text{v}_n$ 가 vector space $V$의 element일 때,  
$\text{Span}(\text{v}_1,...,\text{v}_n)$는 $V$의 subspace이다.

 

---

Linearly Independence

💡
$\text{v}_1,...,\text{v}_n$ 이 $\mathbf{R}^n$ 의 n-vector들이고, $n\times n$ 인 matrix $\text{A}=[\text{v}_1\,\,\,\text{v}_2\,\,\,...\,\,\,\text{v}_n]$ 일 때, 
이 벡터들이 linearly dependent한 것은 $\text{A}$가 singluar 한 것의 필요충분조건이다.  

 

증명)

$c_1\text{v}_1+...+c_n\text{v}_n=0$ 은 matrix equation으로 $\text{A}\text{c}=0$ 으로 나타낼 수 있고,

이 식이 nontrivial solution을 가지려면 $\text{A}$가 singular 해야 한다.($\det(\text{A})=0$)  

 

예제)

Show that the vectors $(1,2,4),(2,1,3),(4,-1,1)$ are linearly dependent in $\mathbf{R}^3$  

 

위 theory에서처럼, 세 개의 벡터로 이루어진 matrix를 만들어보면,

$$ \begin{bmatrix} 1 & 2 & 4 \\ 2 & 1 & -1 \\ 4 & 3 & 1 \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 4 \\ 0 & -3 & -9 \\ 0 & -5 & -15 \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 4 \\ 0 & 1 & 3 \\ 0 & 0 & 0\end{bmatrix} $$

zero row 가 있기 때문에 이 matrix는 singular하고,

따라서 vector들은 linearly dependent하다.  

 

이 이론은, vector들이 주어졌을 때, minimal spanning set이 되느냐? 하고 물었을 때 사용하기 적합하다.  

 

💡
$\text{v}_1,...,\text{v}_n$ 이 vector space $V$의 vector들일 때, 
vector $\text{v}\in\text{Span}(\text{v}_1,...,\text{v}_n)$이 $\text{v}_1,...,\text{v}_n$의 linear combination으로 unique하게 쓸 수 있는 건 
$\text{v}_1,...,\text{v}_n$가 linearly independent한 것의 필요충분조건이다.  

---

Basis and Demension

Basis

💡
Nonzero vector space $V$의 nonempty subset $B$ 는 아래 두 조건을 만족하면 $V$의 basis이다.

- $B$가 linearly independent하고,$B$가 $V$를 span하면,  
- $B$가 linearly independent하고,$B$가 $V$를 span하면,  

 

예제) Show that $B$ is a basis of $\mathbf{R}^3$

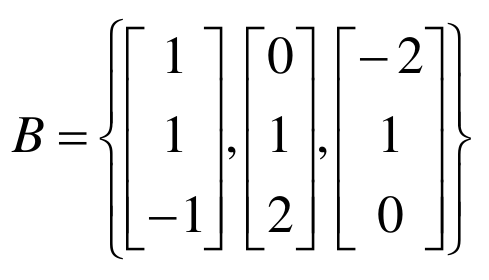
위 vector들로 이루어진 matrix를 만들어 보면,

$$ \text{A}=\begin{bmatrix} 1 & 0 & -2 \\ 1 & 1 & 1 \\ -1 & 2 & 0 \end{bmatrix}\sim\begin{bmatrix} 1 & 0 & -2 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{bmatrix}=\text{U} $$

각 열이 pivot column이므로, free variable이 없다.

따라서 $B$는 linearly independent하다.

또한, 각 row가 pivot position을 가지고 있으므로, $B$는 $\mathbf{R}^3$를 span한다.

💡 $\text{v}_1,...,\text{v}_n$ 이 vector space $V$의 vector들일 때, $m>n$ 인 $V$의 $m$개의 벡터들의 집합은 linearly dependent할 수 밖에 없다.

💡 만약 $\{\text{v}_1,...,\text{v}_n\}$ 와 $\{\text{u}_1,...,\text{u}_m\}$ 둘 다 vector space $V$ 의 basis라면, $n=m$ 이다.

 

Dimension

💡 Vector space $V$가 n개의 원소로 이루어진 basis를 갖고 있다면, $V$는 finite-dimensional이라 부르고, $n$을 $V$의 dimension이라고 한다.
$$ \dim(V)=n $$