본 포스팅은 유튜브 채널 이상엽Math를 참고하였습니다.
벡터와 좌표계
평면벡터


공간벡터

n차원 벡터
- 영벡터
→0=0=(0,0,⋯,0) - 두 벡터
v=(v1,⋯,vn),w=(w1,⋯,wn) ⇔v1=w1,⋯,vn=wn
벡터의 연산
Norm
- 벡터의 크기(또는 길이)라고도 하며, 수식으로는
‖v‖=√v21+v22+⋯+v2n - 일반적으로
L2 - Norm이 1인 벡터를 단위벡터라고 함.
- 정규화 :
v‖v‖
- 정규화 :
e1=(1,0,⋯,0),e2=(0,1,⋯,0)
선형결합
벡터의 덧셈과 뺄셈

벡터의 실수배

선형(일차)결합
스칼라 곱
한 벡터가 다른 벡터의 방향에 대해 가한 힘에 의해 변화된 스칼라(크기).
점곱 또는 내적이라고 함(Dot product, Inner product)
(

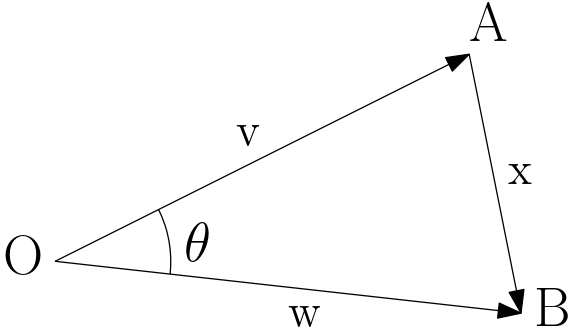
→ 제2코사인 법칙으로 증명 가능
제2 코사인 법칙에 따라
⚠️ 벡터의 연산 성질
벡터 곱
방향은 두 벡터에 동시에 수직이고, 크기는 두 벡터의 평행사변형의 면적인
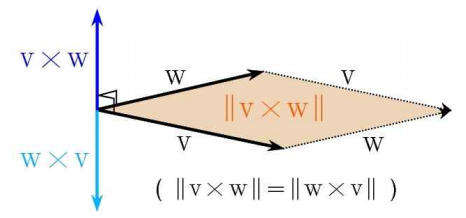
위 식도 determinant구하는 거랑 유사하게 생각하면 됨. 각 위치의 원소 가려주면 됨.
(방향은 오른손 법칙 생각하면 됨. cross product의 앞에 벡터부터 오른손으로 감아쥐었을 때 엄지가 향하는 방향)
ex.
⚠️ 벡터 곱의 성질
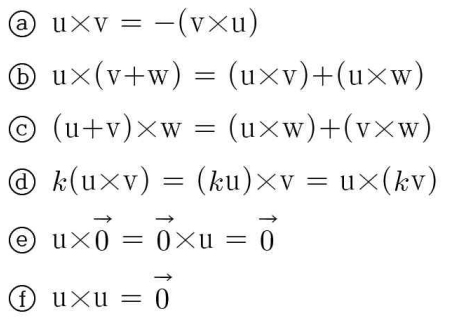
결합법칙은 적용이 안됨.
→
벡터의 응용
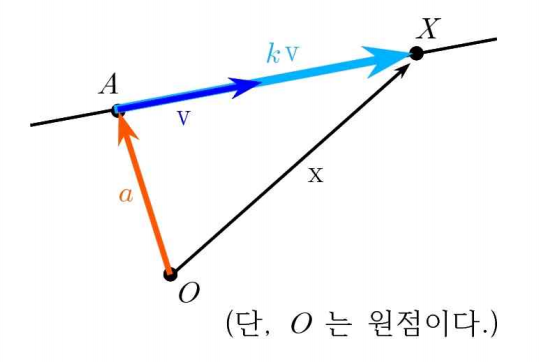
직선의 표현
x=a+kv
을 만족한다.(단,
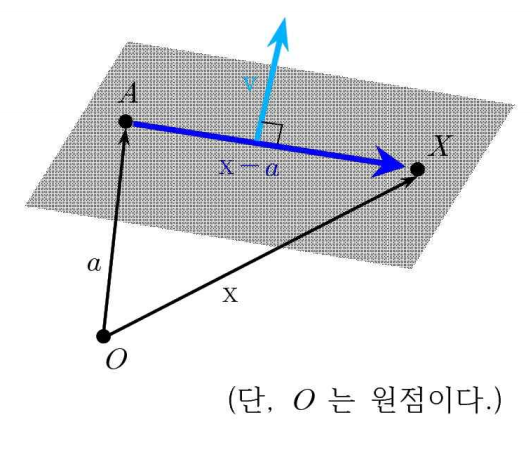
평면의 표현
(x−a)⋅v=0
을 만족한다.
(법선벡터는 평면상의 서로 다른 두 직선의 방향벡터들의 벡터 곱으로 구하면 쉬움)
Miscellaneous

두 벡터
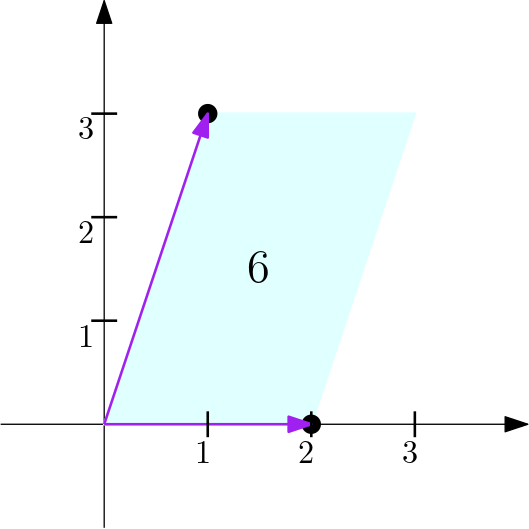
너비가 6이 되고,
즉, 두 벡터를 나열한 matrix의 determinant의 절대값이 두 벡터로 만들어지는 평행사변형의 너비임을 유추할 수 있다.
더 수학적으로 따져보면,

/ /문제제기 및 피드백 언제든지 감사히 받겠습니다.
