최적화 문제

곡선 적합

보간법(Interpolation)

개념

주어진 특정 점들을 포함하는 함수를 구하는 방법.

💡 좌표평면에 있는 임의의 서로 다른 $n$개의 점을 지나는 $k$차 다항함수는 유일하게 존재한다. (단, $k$는 $k<n$ 인 자연수)

보간법은 좀 제한적인 개념이다.

즉, 해당 $n$개의 점들을 만족하는 다항함수가 없을 수도 있다.

만약 있다면, 이는 유일하다는 의미이다.  

 

사례

네 점 $(1,3),(2,-2),(3,-5),(4,0)$ 을 모두 지나는 3차 함수

$$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3$$

을 구하자. 우선 다음의 방정식을 세운다.  

 

① $\left(\begin{array}{cccc}1& x_1& x_1^2& x_1^3\\ 1& x_2& x_2^2& x_2^3\\ 1& x_3& x_3^2& x_3^3\\ 1& x_4& x_4^2& x_4^3\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\\ a_3\end{array}\right)=\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\end{array}\right)$  

 

② 네 점을 대입하고 augmented matrix(첨가행렬)을 만든다.

$\left(\begin{array}{ccccc}1& 1& 1& 1& 3\\ 1& 2& 4& 8& -2\\ 1& 3& 9& 27& -5\\ 1& 4& 16& 64& 0\end{array}\right)$  

 

③ 첨가행렬을 가우스-조던 소거법을 이용해 푼다.

$\left(\begin{array}{ccccc}1& 1& 1& 1& 3\\ 1& 2& 4& 8& -2\\ 1& 3& 9& 27& -5\\ 1& 4& 16& 64& 0\end{array}\right)\Rightarrow \left(\begin{array}{ccccc}1& 0& 0& 0& 4\\ 0& 1& 0& 0& 3\\ 0& 0& 1& 0& -5\\ 0& 0& 0& 1& 1\end{array}\right)$  

 

④ $a_0=4,a_1=3,a_2=-5,a_3=1$ 이므로 $f(x)=4+3-5x^2+x^3$ 이다.

 

앞에서도 설명했지만 보간법의 치명적인 단점은, 유연성이 부족하다.

즉, 머신러닝 용어로 overfitting의 위험이 높다.  

  

최소제곱법(Least squares)

개념

특정 점들을 포함하는 함수를 특정 지을 수 없을 때,

실제 해와의 오차 제곱 합이 최소가 되는 근사적인 해를 구하는 방법.

(보간법처럼 딱 맞을 필요가 없으니 유연성이 좋다)

💡 방정식 $A\text{x}=B$ 을 변형한 방정식 $A^{T}A\text{x}=A^{T}B$ (정규방정식)의 모든 해는 $A\text{x}=B$의 최소제곱해이다.

  

사례

네 점 $(0,1),(1,3),(2,4),(3,4)$ 에 근사하는 일차함수

$$f(x)=a_0+a_{1}x$$

을 구하자. 우선 다음의 방정식을 세운다.  

 

① $A\text{x}=B$

$\left(\begin{array}{cc}1& x_1\\ 1& x_2\\ 1& x_3\\ 1& x_4\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\end{array}\right)=\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\end{array}\right)$  

 

② 네 점을 대입하고 정규방정식 $A^{T}A\text{x}=A^{T}B$로부터 방정식 $\text{x}=(A^{T}A{)}^{-1}{A}^{T}B$을 구성한다.

$A^{T}A=\left(\begin{array}{cc}4& 6\\ 6& 14\end{array}\right)$ 이므로

$(A^{T}A{)}^{-1}={\left(\begin{array}{cc}4& 6\\ 6& 14\end{array}\right)}^{-1}={\displaystyle \frac{1}{10}}\left(\begin{array}{cc}7& -3\\ -3& 2\end{array}\right)$

$\therefore \text{x}={\displaystyle \frac{1}{10}}\left(\begin{array}{cc}7& -3\\ -3& 2\end{array}\right)\left(\begin{array}{cccc}1& 1& 1& 1\\ 0& 1& 2& 3\end{array}\right)\left(\begin{array}{c}1\\ 3\\ 4\\ 4\end{array}\right)$  

 

③ $\text{x}=\left(\begin{array}{c}{a}_0\\ a_1\end{array}\right)=\left(\begin{array}{c}\frac{3}{2}\\ 1\end{array}\right)$ 이므로 구하고자 하는 함수는 $f(x)={\displaystyle \frac{3}{2}}+x$ 이다.

 

$n$차 일반화

$m$개의 자료점 $(x_1,y_1),\cdots ,(x_m,y_m)$에 대해 $n$차 다항식 $y=a_0+a_{1}x+\cdots +a_n{x}^n$을 최소제곱법으로 이용하여 근사하기 위해서는 $A\text{x}=B$를

$$A=\left(\begin{array}{cccc}1& x_1& \cdots & x_1^n\\ 1& x_2& \cdots & x_2^n\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_m& \cdots & x_m^n\end{array}\right),\text{x}=\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right),B=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right)$$

로 설정하면 된다.  

 

사실, 위와 같은 꼴의 다항식이 아니라 만약 식이 $xy,\log x,\sin x$ 등의 항이 있다 하더라도 똑같이 적용가능하므로 굉장히 유용하다.  

 

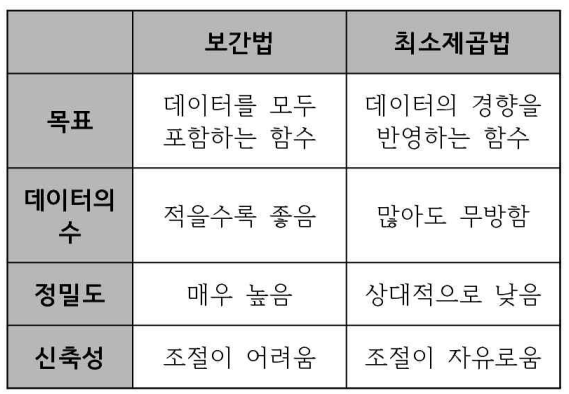
두 방법의 비교

  

 

---

이차형식의 최적화

이차형식(Quadratic form)

가환환 $K$ 위의 가군 $V$에 대해 다음 세 조건을 만족시키는 함수 $Q:V\to K$

$\mathrm{\forall }k,l\in K,\mathrm{\forall }u,v,w\in V,$

1. $Q(kv)=k^{2}Q(v)$
2. $Q(u+v+w)=Q(u+v)+Q(v+w)+Q(u+w)-Q(u)-Q(v)-Q(w)$
3. $Q(ku+lv)=k^{2}Q(u)+l^{2}Q(v)+klQ(u+v)-klQ(u)-klQ(v)$  

 

예1) $R^2$ 상의 일반적인 이차형식은 다음과 같다.

$$a_1{x}_1^2+a_2{x}_2^2+2a_3{x}_1{x}_2\iff \left(\begin{array}{cc}{x}_1& x_2\end{array}\right)\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_2\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$$  

 

예2) $R^3$ 상의 일반적인 이차형식은 다음과 같다.

$$\begin{gathered} a_1{x}_1^2+a_2{x}_2^2+a_3{x}_3^2+2a_4{x}_1{x}_2+2a_5{x}_1{x}_3+2a_6{x}_2{x}_3 \\ \iff \left(\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right)\left(\begin{array}{ccc}{a}_1& a_4& a_5\\ a_4& a_2& a_6\\ a_5& a_6& a_3\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right) \end{gathered}$$  

 

제약된 극값

개념

특정 제약(constraint) 하에 결정되는 원하는 식의 최댓값 또는 최솟값.

💡 $n\times n$ 행렬 $A$의 eigenvalue를 큰 순서대로 ${\lambda }_1,\cdots ,{\lambda }_n$ 이라 하자. 이 때 $\Vert \text{v}\Vert =1$ 제약 하에 ${\text{v}}^{T}A\text{v}$ 의 최댓(솟)값은 ${\lambda }_1({\lambda }_n)$에 대응하는 단위고유벡터에서 존재한다.

  

사례

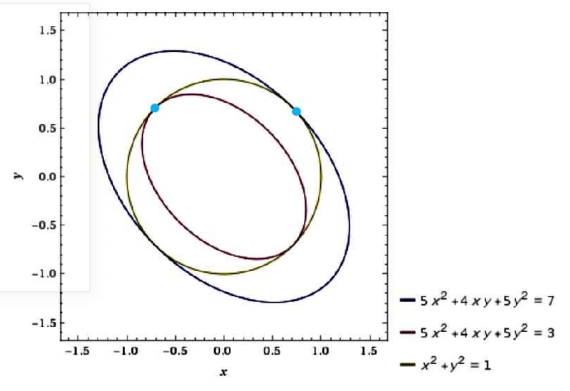
제약 $x^2+y^2=1$ 하에서 $z=5x^2+5y^2+4xy$ 의 최댓값과 최솟값을 구하자.

우선 $z$를 이차형식 ${\text{v}}^{T}A\text{v}$ 형태로 변환한다.  

 

① $$\begin{gathered} a_1{x}^2+a_2{y}^2+2a_{3}xy \\ \iff \left(\begin{array}{cc}{x}_1& x_2\end{array}\right)\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_2\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)={\text{v}}^{T}A\text{v} \end{gathered}$$

즉, $z=\left(\begin{array}{cc}x& y\end{array}\right)\left(\begin{array}{cc}5& 2\\ 2& 5\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$  

 

② 행렬 $A=\left(\begin{array}{cc}5& 2\\ 2& 5\end{array}\right)$ 의 eigenvalue와 eigenvector를 구한다.

$$\begin{gathered} {\lambda }_1=7,{\text{v}}_1=(1,1) \\ {\lambda }_2=3,{\text{v}}_2=(-1,1) \end{gathered}$$  

 

③ Eigenvector를 정규화한다.

$$\begin{gathered} {\lambda }_1=7,{\text{v}}_1=({\displaystyle \frac{1}{\sqrt{2}}},{\displaystyle \frac{1}{\sqrt{2}}}) \\ {\lambda }_2=3,{\text{v}}_2=(-{\displaystyle \frac{1}{\sqrt{2}}},{\displaystyle \frac{1}{\sqrt{2}}}) \end{gathered}$$  

 

④ 따라서 $(x,y)=({\displaystyle \frac{1}{\sqrt{2}}},{\displaystyle \frac{1}{\sqrt{2}}})$ 일 때 $z$는 최댓값 $7$을 갖고,

$(x,y)=(-{\displaystyle \frac{1}{\sqrt{2}}},{\displaystyle \frac{1}{\sqrt{2}}})$ 일 때 $z$는 최솟값 $3$을 갖는다.  

 

※ 물론 nomalize안해도 최대 최소값은 변함없다.